![]() 平面において,原点Oを通る半径
平面において,原点Oを通る半径 ![]() の円を
の円を![]() とし,
その中心をAとする.
Oを除く
とし,
その中心をAとする.
Oを除く![]() 上の点Pに対し,次の2つの条件(a), (b)で定まる点Qを考える.
上の点Pに対し,次の2つの条件(a), (b)で定まる点Qを考える.
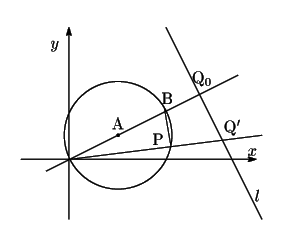
方針
解1
(1)
![]() を
を![]() が円
が円![]() の直径となる点とし,
半直線
の直径となる点とし,
半直線![]() 上の点
上の点![]() を
を
![]() のとき
のとき
つまり点![]() が円
が円![]() 上を動けば,点
上を動けば,点![]() は直線
は直線![]() 上を動く.
逆に,直線
上を動く.
逆に,直線![]() 上の点
上の点![]() があれば,
半直線
があれば,
半直線![]() と円
と円![]() は原点および他の点で交わり,条件を満たす点
は原点および他の点で交わり,条件を満たす点![]() を定める.
を定める.
よって点![]() の軌跡が直線
の軌跡が直線![]() である,
である,
(2)
原点を中心とする半径1の円を![]() とする.
とする.
![]() より,
より,
![]() なら
なら
![]() である.つまり点
である.つまり点![]() が円
が円![]() の内部にあれば点
の内部にあれば点![]() は円
は円![]() の外部にある.
同様に点
の外部にある.
同様に点![]() が円
が円![]() の外部にあれば点
の外部にあれば点![]() は円
は円![]() の内部にあり,
点
の内部にあり,
点![]() が円
が円![]() の周上にあれば点
の周上にあれば点![]() は点
は点![]() と一致する.
と一致する.
したがって円![]() が円
が円![]() の内部にあれば
の内部にあれば![]() と
と![]() に共通点はない.
円
に共通点はない.
円![]() が円
が円![]() に内接すれば
に内接すれば![]() と
と![]() は1点を共有する.
円
は1点を共有する.
円![]() が円
が円![]() と交われば,
と交われば,![]() はこの交点を通り,したがって
はこの交点を通り,したがって![]() と
と![]() は2点で交わる.
つまり
は2点で交わる.
つまり![]() と
と![]() が2点で交わることが求める条件である.
が2点で交わることが求める条件である.
その条件は
解2
記号は解法1のものを使う.
(1)
条件から正の数![]() を用いて
を用いて
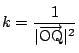 となり
となり
円![]() は線分
は線分![]() を直径とする円なので,
点
を直径とする円なので,
点![]() が円
が円![]() 上にあることは
上にあることは
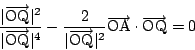
(2)
![]() が
が![]() と2点で交わる条件は,
円
と2点で交わる条件は,
円![]() の中心
の中心![]() と
と![]() との距離が半径
との距離が半径![]() より小さいことである.
より小さいことである.
(1)から![]() と
と![]() との距離は
との距離は
![]() であり,
であり,![]() から
から
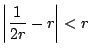 .
つまり
.
つまり
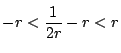 となり,求める
となり,求める
解3 (1)
![]() ,
,
![]() とし,
とし,
![]() を成分で書く.
を成分で書く.
円![]() の中心を
の中心を![]() とする.原点を通るので,
とする.原点を通るので,![]() である.
円
である.
円![]() は円の方程式
は円の方程式
![]() を展開整理して代入する.条件から
を展開整理して代入する.条件から
![]() なので
なので
(2)
![]() が
が![]() と2点で交わる条件は,
円
と2点で交わる条件は,
円![]() の中心
の中心![]() と
と![]() との距離が半径
との距離が半径![]() より小さいことである.
より小さいことである.
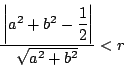
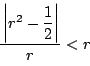
解4
(1)
図形を複素数平面で考え,
![]() とおく.
条件から正の数
とおく.
条件から正の数![]() を用いて
を用いて![]() とおけ,さらに条件から
とおけ,さらに条件から
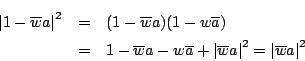
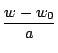 が純虚数となったので,
直線
が純虚数となったので,
直線
(2) はベクトルの場合と同様なので省略する. □
吟味
点Qは,点Pの,原点を中心とする半径1の円に関する反転 または鏡像である,という.
反転を扱うには,図形的方法とベクトルや座標,あるいは複素数平面による方法がある. 解法1は,若干異なるが,ベクトルを用いた解法2と座標による解法3は,本質的には同じことで,表現が異なるだけである.
ベクトルでは
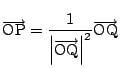 までしかできないが,複素数では
までしかできないが,複素数では
![]() まで簡明になるので,逆に解いて代入することが可能になる.このように反転を座標平面で扱うときは,複素数平面として考えるのが一番簡明でである.
まで簡明になるので,逆に解いて代入することが可能になる.このように反転を座標平面で扱うときは,複素数平面として考えるのが一番簡明でである.