次: 正像法・逆像法［典型問題］ 上: 平面図形のとらえ方 前: 内接円と外接円［06京大理系］

点の存在［01京大改題］

問題     

$xyz$空間内に，異なる$n$個の点 $\mathrm{P}_1$，$\mathrm{P}_2$，...，$\mathrm{P}_n$と ベクトル $\overrightarrow{v}$があり，$k\ne m$のとき $\overrightarrow{\mathrm{P}_k\mathrm{P}_m}\cdot\overrightarrow{v}\ne 0$ が成り立っているとする．このとき，$k$と異なるすべての$m$に対し

$$\overrightarrow{\mathrm{P}_k\mathrm{P}_m}\cdot\overrightarrow{v}<0$$

が成り立つよう な点$\mathrm{P}_k$が存在することを示せ．

方針 これは平面，空間に関係ない問題であるのでここに含める．

1.

ベクトル $\overrightarrow{v}$となす角がすべて鈍角であるような 始点がとれればよい． つまり， $\overrightarrow{v}$と直交する方向に関して， $\overrightarrow{v}$とは逆の方向であればよい．

2.

問題の条件も結論も，始点がいろいろ変化する． このようなときに，始点を固定して考えるのは， ベクトルの論証の基本だ． 条件も得たい結論もすべて始点を$\mathrm{O}$にとって書いてみる．

解1

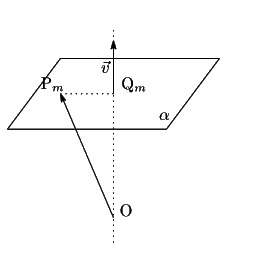図のようにベクトル $\vec{v}$ と垂直な平面 $\alpha$ を考える． この平面をベクトル $\vec{v}$ の方向に平行移動していく． すると， $n$ 個の点$\mathrm{P}_1$，$\mathrm{P}_2$，...，$\mathrm{P}_n$ のどれかが最初に $\alpha$ 上に来るときと，最後に $\alpha$ から離れるときがある．

$\alpha$ 上のベクトルはすべてベクトル $\vec{v}$ と垂直である．したがって $k\ne m$のとき $\overrightarrow{\mathrm{P}_k\mathrm{P}_m}\cdot\overrightarrow{v}\ne 0$ が成り立っているので，同時に二つの点が $\alpha$ 上に来ることはない． 最後に $\alpha$ から離れるときの点を $\mathrm{P}_k$ とする．

ベクトル $\vec{v}$ の始点を $\alpha$ 上においたとき $k$と異なるすべての$m$に対しベクトル $\overrightarrow{\mathrm{P}_k\mathrm{P}_m}$ は始点が $\alpha$ 上にあり，かつ $\alpha$ に関してベクトル $\vec{v}$ とは反対の側にある．

したがってベクトル $\overrightarrow{\mathrm{P}_k\mathrm{P}_m}$とベクトル $\vec{v}$ の なす角はすべて鈍角である．つまり $k$と異なるすべての$m$に対し

$$\overrightarrow{\mathrm{P}_k\mathrm{P}_m}\cdot\overrightarrow{v}<0$$

が成り立つ．□

解2
基準点 $\mathrm{O}$ をとる． $k\ne m$ なら $\overrightarrow{\mathrm{P}_k\mathrm{P}_m}\cdot\overrightarrow{v}\ne 0$ なので，

$$\overrightarrow{\mathrm{P}_k\mathrm{P}_m}\cdot\overrightarro... ... -\overrightarrow{\mathrm{OP}_k}\cdot \overrightarrow{v} \ne 0$$

よって

$$\overrightarrow{\mathrm{OP}_m}\cdot \overrightarrow{v}\ \ (m=1,\ 2,\ \cdots,\ n )$$

はすべて互いに異なる．したがって，このなかに 最大のものがただ一つ存在する． それを $O\overrightarrow{\mathrm{P}_k}\cdot \overrightarrow{v}$ とする． このとき $k\ne m$ なら

$$\overrightarrow{\mathrm{P}_k\mathrm{P}_m}\cdot\overrightarro... ...w{v} -\overrightarrow{\mathrm{OP}_k}\cdot \overrightarrow{v}<0$$

である． $\mathrm{P}_k$ が題意をみたす点である．□

吟味

こちらは図形的な性質を使っていないので， この二つの証明はずいぶん違うように見える． しかし，次のように考えると， それほどちがったことをしているのではないことに気づく．

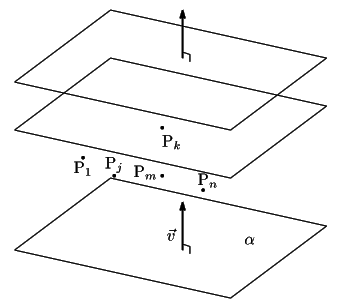ベクトル $\vec{v}$ は長さが1としても一般性を失わない．このとき内積 $\overrightarrow{\mathrm{OP}_m}\cdot\vec{v}$ は何を意味するか．

$\mathrm{P}_m$ から，$\mathrm{O}$を通り$\vec{v}$ に平行な直線に下ろした点 を $\mathrm{Q}_m$ とすると，

$$\overrightarrow{\mathrm{OP}_m}\cdot\vec{v}=\mathrm{OQ}_m$$

だ． 解法1で，最後に $\alpha$ から離れる点は，$\mathrm{OQ}_m$が一番長い点であり， これは解法2で， $\overrightarrow{\mathrm{OP}_m}\cdot\vec{v}$が最大になる点である． ゆえに解法1と解法2は同じことをやっている．

このように別解というのは，同じ数学的な現象をいろんな側面から見ることで生まれる． しかしまた，その数学的な現象に対する理解が深まれば，それほど別でもないということがわかる． あるいは，二つの方法に共通なことは何かを考えることで 数学的な現象に対する理解が深まる，ということもある．