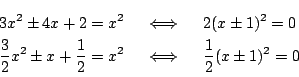上: 内部構造の分析
前: 考え方
上: 内部構造の分析
前: 考え方
解答 1.1
問題
1.1
解1
を
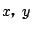
の連立方程式と見て解く.
であるから
したがって,
これを最初の式に代入して
解2
条件式①から 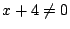 のとき,
のとき,
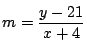 .
.
これを②に代入して
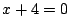
のとき,①から
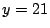
.この
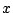
と
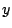
を2に代入すると,
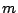
の値が存在する.
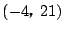
は軌跡の点.
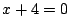
のとき,②から
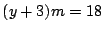
.
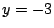
のときに限り
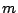
が存在しない.
つまりいかなる,
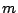
をもってしても
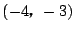
は解になり得ない.
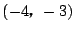
は除外点.
解3
それぞれの方程式は
\[
\left\{
\begin{array}{l}
m(x+4)-y+21=0 \\
x-14+m(y+3)=0
\end{array}
\right.
\]
と変形でき,それぞれ定点$(-4,\ 21)$と$(14,\ -3)$を通る.
かつ,
\[
m\cdot 1+(-1)m=0
\]
より,2直線は直交している.
第一の直線は,定点のまわりを $ y $ 軸平行となる以外で回転する.
第二の直線は,定点のまわりを $ x $軸平行となる以外で回転する.
したがって,交点の軌跡は,二定点を直径とする円であり,かつ
いかなる $ m $ をもってしても交点が $ (-4,\ -3) $ にはならない. $ (-4,\ -3) $ は除外点.
\[
(x-5)^2+(y-9)^2=15^2 \quad ただし点(-4,\ -3)を除く
\]
□
解答 1.2
問題
1.2
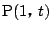 ,
,
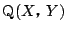 とする.条件 1.2.から
とする.条件 1.2.から 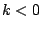 を用いて
を用いて
とおける.条件 3.から
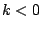
より
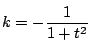
なので,
これから
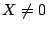
で,
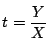
.これを2式のいずれかに代入して整理すると
求める軌跡は
□
解答 1.3
問題
1.3
-
- (1)
-
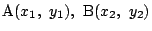 とする.
とする.
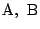 における接線は
における接線は
これが, いずれも
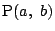 を通るので
を通るので
条件①は直線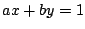 が
が
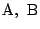 を通ることを示している.
したがって, 直線
を通ることを示している.
したがって, 直線 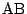 の式は
の式は
一方①の2式を引くことにより,
また
の辺々を引いて
②,③から
ゆえに AB の中点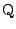 は直線
は直線
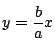 上にある.
上にある.
したがって 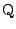 は2直線,
は2直線,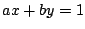 と
と
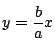 の交点である.
の交点である.
これから
別解
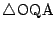 と
と
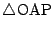 は相似である.
は相似である.
つまり
とおける.④に代入して
- (2)
- 点 Q
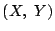 とおく.
とおく.
ここで
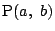 が円
が円 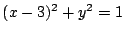 上を動くので
上を動くので
ここで
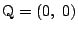 のときは A, B での接線は平行になるので
のときは A, B での接線は平行になるので
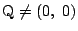 .つまり
.つまり 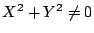 .これに注意して整理すると
.これに注意して整理すると
求める軌跡は次の円である.
□
解答 1.4
問題
1.4
条件式を逆に解く. 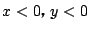 のとき2式の分母はともに0でないので,
のとき2式の分母はともに0でないので,
この2式を
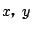
の連立方程式として整理すると,
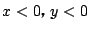
より
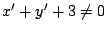
のとき
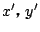
の満たすべき条件は
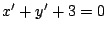
のとき2式に
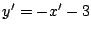
を代入して整理すると
となり,①と両立しない.よって
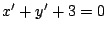
となる
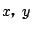
は存在しない.
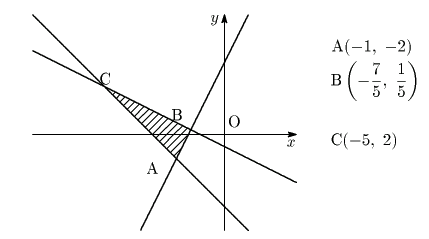 3直線の交点を
3直線の交点を
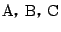 とすると,
とすると,
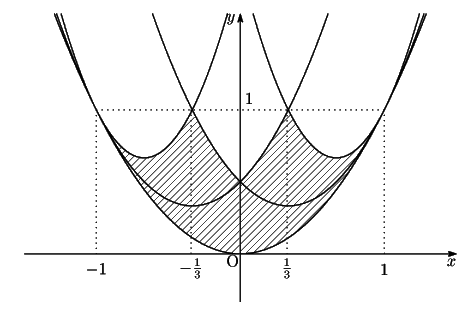
より求める領域は左図のようになる.
(訂正:「A(-1,-2)」を「A(-2,-1)」に)
(訂正:Iをiに,2カ所.「-x+1」を「-x-1」に)
ここで,
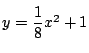
と
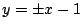
は,
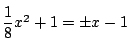
より,
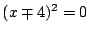
となるので, 接する.
□
注意
最初の考察で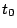 を用いた行は,実際の解答には書かなくてもよい.また
を用いた行は,実際の解答には書かなくてもよい.また 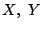 を用いているところも,はじめから,固定された点
を用いているところも,はじめから,固定された点 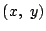 と座標系の
と座標系の 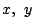 を
あえて混同して,
を
あえて混同して, 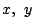 のままでよい.
のままでよい.
したがって,
「点 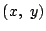 が求める通過領域にあることと,
二次方程式
が求める通過領域にあることと,
二次方程式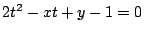 が
が 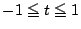 に解をもつことは同値である.」
に解をもつことは同値である.」
のような論述でよい.
解答 1.6
問題
1.6
直線ABの式は
点
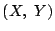
が通過領域にあるのは,
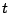
についての方程式
が
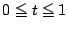
に解をもつことと同値である.
とおく.
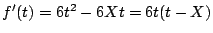
である.したがって,その条件は
これから、
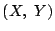
が通過領域の点であるための必要十分条件は
よって求める領域は
(訂正:「x3+3x」を「x3-3x」に)
それを図示する.
□
注意
点 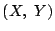 は,はじめから点と座標系をあえて混同して
は,はじめから点と座標系をあえて混同して 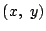 で,論述してもよい.
次の解答はそのようにする.
で,論述してもよい.
次の解答はそのようにする.
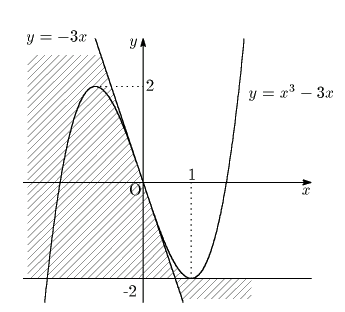
解答 1.7
問題
1.7
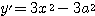 で
で 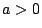 であるから
であるから 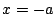 で極大,
で極大, 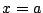 で極小である.
で極小である.
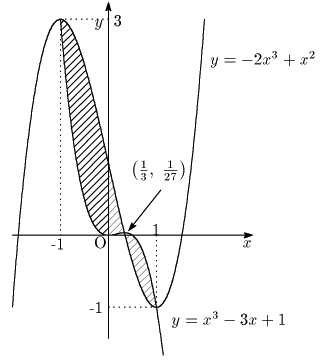 したがって点
したがって点 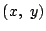 が求める領域の点であることは,
が求める領域の点であることは,
を満たす
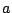
が存在することと同値である.
すなわち
となる
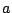
が存在すればよい.
それを図示する.
□
解答 1.9
問題
1.9
-
- (1)
- 二つの放物線
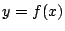 と
と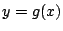 が二つの共有点をもつことは,
それらの曲線の方程式を連立させて
が二つの共有点をもつことは,
それらの曲線の方程式を連立させて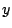 を消去した
を消去した
が,相異なる二つの実数解をもつことと同値である.
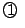 を整理して
を整理して
したがって
これから
- (2)
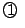 の二つの解を
の二つの解を
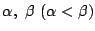 とする.
解と係数の関係から
とする.
解と係数の関係から
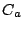 の面積を
の面積を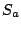 とすると
とすると
ここで
- (3)
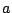 が(1)で求めた範囲を動くとき,点
が(1)で求めた範囲を動くとき,点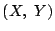 が,
少なくとも1つの
が,
少なくとも1つの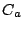 に属するための必要十分条件は
に属するための必要十分条件は
となる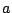 が存在することである.
が存在することである.
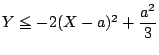 は
は
である.ここで
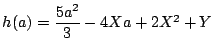 とおく.
とおく.
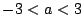 の範囲で
の範囲で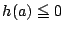 となる
となる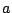 が存在する条件は,
軸
が存在する条件は,
軸
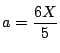 で場合に分けて
で場合に分けて
 これから変数を
これから変数を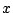 と
と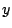 にして
にして
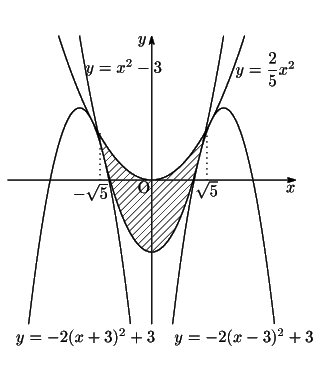
これと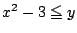 の共通領域が,条件を満たす点の集合である.
の共通領域が,条件を満たす点の集合である.
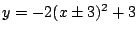 と
と
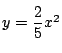 は
は
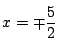 で接し,
で接し,
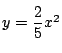 と
と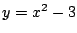 は
は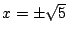 で交わる.また
で交わる.また
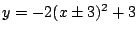 と
と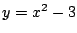 は
は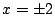 で接する.このことに注意して
図示すると右のようになる.
で接する.このことに注意して
図示すると右のようになる.
ゆえにその面積は
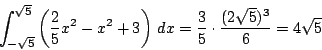
□
解答 1.10
問題
1.10
(1)
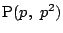 ,
,
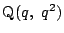 とおく.
線分 PQ を1:2に内分する点Rの座標を
とおく.
線分 PQ を1:2に内分する点Rの座標を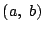 とする.
このとき,
とする.
このとき,
である.
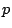
を
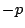
に,
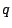
を
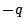
に置きかえると
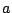
は
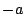
になり,
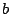
は変化しない.よって領域
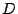
は
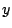
軸に関して対称であり,
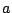
を
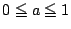
の範囲で固定して考えればよい.
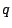 を消去して
を消去して
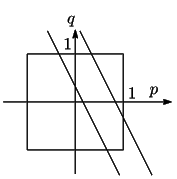 ここで
ここで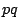 平面に直線
平面に直線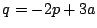 と領域
と領域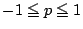 ,
,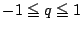 を図示して
を図示して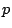 の変域を求める.
の変域を求める.
直線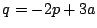 と領域
と領域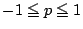 ,
,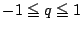 の共有部分が
の共有部分が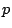 の変域を与える.
の変域を与える.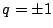 のとき
のとき
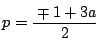 なので,図から
なので,図から
となる.
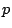
がこの変域を動くときの
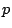
の2次関数
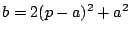
の値域が,
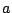
を固定したとき点
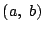
が
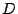
に属するための
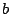
の条件である.
軸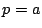 は条件
は条件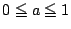 によってつねに
によってつねに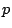 の変域の内にある.
よって
の変域の内にある.
よって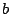 の最小値はつねに
の最小値はつねに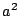 である.
また
である.
また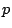 の変域の中点はそれぞれ
の変域の中点はそれぞれ
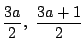 であり,
であり,
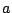 はこれより小さいので,最大値は変域の右端でとる.
はこれより小さいので,最大値は変域の右端でとる.
である.対称性を考え
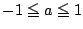
における
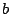
の条件は次のようになる.
これから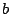 の条件を
の条件を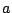 で表すと,
で表すと,
(2)
これを満たす
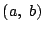
の集合が
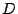
である.
これを図示すればよい.
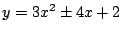 と
と
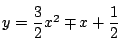 は
は
から
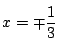
で交わる.また
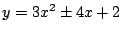
と
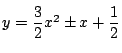
の
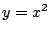
との位置関係は
よりともに
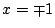
で接する.
以上をもとに図示すると次のようになる.
□
$ \mathrm{P}(p,\ p^2) $ , $ \mathrm{Q}(q,\ q^2) $ とおく.
線分 PQ を1:2に内分する点Rの座標を $ (a,\ b) $ とする.
このとき,
\[
a=\dfrac{2p+q}{3},\
b=\dfrac{2p^2+q^2}{3}
\]
である.点 $ (a,b) $ が $ D $ に属することは,
これを満たす $ p,\ q $ が $ -1\leqq p,\ q\leqq 1 $ に存在することと同値である.
これから $ q $ と $ p $ を消去して2つの2次方程式を得る.
\begin{eqnarray*}
&&6p^2-12ap+9a^2-3b=0\\
&&3q^2-6aq+9a^2-6b=0
\end{eqnarray*}
定数を約した方程式の左辺を $ f(p),\ g(q) $ とおく.
\begin{eqnarray*}
f(p)&=&2p^2-4ap+3a^2-b\\
g(q)&=&q^2-2aq+3a^2-2b
\end{eqnarray*}
求める $ a $ と $ b $ の条件は次のようになる.
(*) $ f(p)=0,\ g(q)=0 $ が $ -1\leqq p,\ q \leqq 1 $
の範囲に関係式 $ a=\dfrac{2\alpha+\beta}{3} $ を満たす解 $ \alpha $ と $ \beta $ をもつ.
$ f(p)=0 $ と $ g(q)=0 $ は $ a=\dfrac{2p+q}{3} $ の置きかえで相互に変わるので
$ f(p)=0 $ の2つの解の一方と $ g(q)=0 $ の2つの解の一方,
$ f(p)=0 $ の2つの解の他方と $ g(q)=0 $ の2つの解の他方はそれぞれ
関係式 $ a=\dfrac{2p+q}{3} $ を満たしている.
したがって条件(*)が成立するのは次のいずれかの場合である.
(i)
$ f(p)=0 $ が $ -1\leqq p \leqq 1 $ に1解をもち他の解が $ p\leqq -1 $ にあり,
$ g(q)=0 $ が $ -1\leqq q \leqq 1 $ に2解をもつか,
1解をもち他の解が $ 1\leqq q $ にある.
\begin{eqnarray*}
&&f(-1)\geqq 0,\ f(1)\leqq 0\\
&かつ&g(-1)\geqq 0,\ g(1)\geqq 0,\ D_g\geqq 0\
または\ g(-1)\leqq 0,\ g(1)\geqq 0
\end{eqnarray*}
(ii)
$ f(p)=0 $ が $ -1\leqq p \leqq 1 $ に1解をもち他の解が $ 1\leqq p $ にあり,
$ g(q)=0 $ が $ -1\leqq q \leqq 1 $ に2解をもつか,
1解をもち他の解が $ q\leqq -1 $ にある.
\begin{eqnarray*}
&&f(-1)\leqq 0,\ f(1)\geqq 0\\
&かつ&g(-1)\geqq 0,\ g(1)\geqq 0,\ D_g\geqq 0\
または\ g(-1)\geqq 0,\ g(1)\leqq 0
\end{eqnarray*}
(iii)
$ f(p)=0 $ が $ -1\leqq p \leqq 1 $ に2解をもち,
$ g(q)=0 $ が $ -1\leqq q \leqq 1 $ に少なくとも1つの解をもつ.
\begin{eqnarray*}
&&f(-1)\geqq 0,\ f(1)\geqq 0,\ D_f\geqq 0\\
&かつ&g(-1)\geqq 0,\ g(1)\geqq 0,\ D_g\geqq 0\\
&&または\ g(-1)\geqq 0,\ g(1)\leqq 0
\ または\ g(-1)\leqq 0,\ g(1)\geqq 0
\end{eqnarray*}
$ f(p)=0 $ の解が $ p=\pm 1 $ の場合は重なって入っているが,
いずれかの条件を満たせばよいのでかまわない.
\begin{eqnarray*}
f(-1)&=&2+4a+3a^2-b\\
f(1)&=&2-4a+3a^2-b\\
D_f/4&=&2(-a^2+b)\\
g(-1)&=&1+2a+3a^2-2b\\
g(1)&=&1-2a+3a^2-2b\\
D_g&=&2(-a^2+b)
\end{eqnarray*}
なので,条件は次のようになる.
(i)
\begin{eqnarray*}
&&b\leqq 3a^2+4a+2,\ b\geqq 3a^2-4a+2\\
&かつ&
\ b\leqq \dfrac{3}{2}a^2+a+\dfrac{1}{2},\
b\leqq \dfrac{3}{2}a^2-a+\dfrac{1}{2},\ b\geqq a^2\\
&&または\ b\geqq \dfrac{3}{2}a^2+a+\dfrac{1}{2},\
b\leqq \dfrac{3}{2}a^2-a+\dfrac{1}{2}
\end{eqnarray*}
(ii)
\begin{eqnarray*}
&&b\geqq 3a^2+4a+2,\ b\leqq 3a^2-4a+2\\
&かつ&
\ b\leqq \dfrac{3}{2}a^2+a+\dfrac{1}{2},\
b\leqq \dfrac{3}{2}a^2-a+\dfrac{1}{2},\ b\geqq a^2\\
&&または\ b\leqq \dfrac{3}{2}a^2+a+\dfrac{1}{2},\
b\geqq \dfrac{3}{2}a^2-a+\dfrac{1}{2}
\end{eqnarray*}
(iii)
\begin{eqnarray*}
&&b\leqq 3a^2+4a+2,\ b\leqq 3a^2-4a+2,\ b\geqq a^2\\
&かつ&
b\leqq \dfrac{3}{2}a^2+a+\dfrac{1}{2},\
b\leqq \dfrac{3}{2}a^2-a+\dfrac{1}{2},\ b\geqq a^2\\
&&または\
b\leqq \dfrac{3}{2}a^2+a+\dfrac{1}{2},\ b\geqq \dfrac{3}{2}a^2-a+\dfrac{1}{2}\\
&&または\ b\geqq \dfrac{3}{2}a^2+a+\dfrac{1}{2},\
b\leqq \dfrac{3}{2}a^2-a+\dfrac{1}{2}
\end{eqnarray*}
これを満たす $ (a,\ b) $ を図示する.
【以下,図は同じ.またこの図から問(1)の解を求める.】

 上: 内部構造の分析
前: 考え方
Aozora Gakuen
上: 内部構造の分析
前: 考え方
Aozora Gakuen
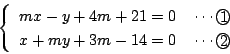
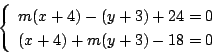
![]() のとき,
のとき,
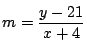 .
.
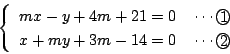
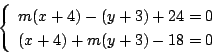
![]() のとき,
のとき,
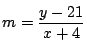 .
.
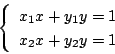
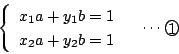
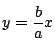 上にある.
上にある.
![]() は2直線,
は2直線,![]() と
と
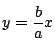 の交点である.
の交点である.
![]() と
と
![]() は相似である.
は相似である.
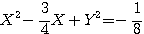
![]() のとき2式の分母はともに0でないので,
のとき2式の分母はともに0でないので,
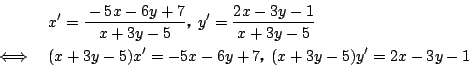
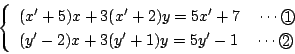
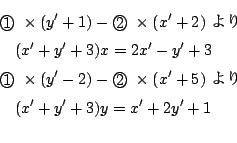
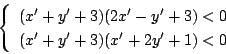
 3直線の交点を
3直線の交点を
![]() とすると,
とすると,
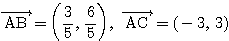
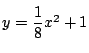 と
と 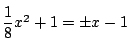 より,
より, ![]() を用いた行は,実際の解答には書かなくてもよい.また
を用いた行は,実際の解答には書かなくてもよい.また ![]() を用いているところも,はじめから,固定された点
を用いているところも,はじめから,固定された点 ![]() と座標系の
と座標系の ![]() を
あえて混同して,
を
あえて混同して, ![]() のままでよい.
のままでよい.
![]() が求める通過領域にあることと,
二次方程式
が求める通過領域にあることと,
二次方程式![]() が
が ![]() に解をもつことは同値である.」
に解をもつことは同値である.」
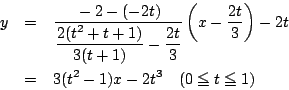
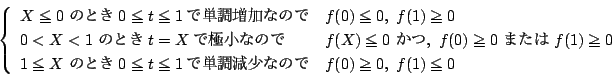
 これから、
これから、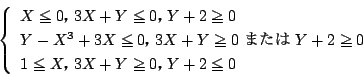
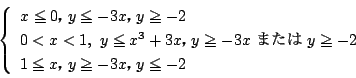
![]() は,はじめから点と座標系をあえて混同して
は,はじめから点と座標系をあえて混同して ![]() で,論述してもよい.
次の解答はそのようにする.
で,論述してもよい.
次の解答はそのようにする.
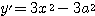 で
で ![]() であるから
であるから ![]() で極大,
で極大, ![]() で極小である.
で極小である.
 したがって点
したがって点 ![]() が求める領域の点であることは,
が求める領域の点であることは,

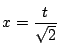 ,
,
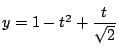 .
点
.
点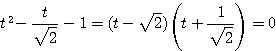
![]() のときは
のときは![]() で条件を満たす.
で条件を満たす.![]() のときは
のときは
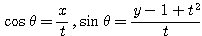
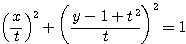
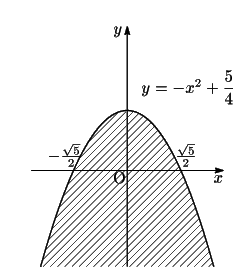 これは
これは![]() をみたす実数
をみたす実数![]() が存在する条件が,点
が存在する条件が,点![]() の満たすべき条件である,
の満たすべき条件である,
![]() とし,
とし,
![]() とする.
とする.![]() の二次方程式
の二次方程式![]() が
負でない解をもてばよい.
が
負でない解をもてばよい.
![]() が必要で,
これから
が必要で,
これから
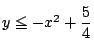 を得る.
を得る.
![]() なので,軸
なので,軸
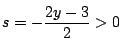 .
ゆえに正の解が存在する.
.
ゆえに正の解が存在する.
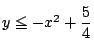 である.
である.
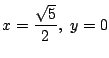 のとき.
のとき.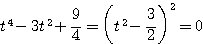
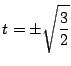 .このとき
.このとき
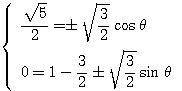
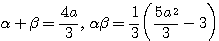
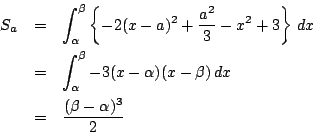
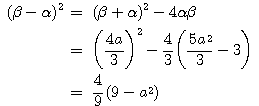
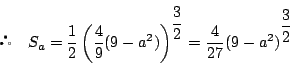
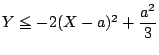 は
は
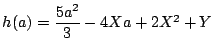 とおく.
とおく.
![]() の範囲で
の範囲で![]() となる
となる![]() が存在する条件は,
軸
が存在する条件は,
軸
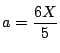 で場合に分けて
で場合に分けて
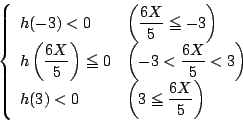
 これから変数を
これから変数を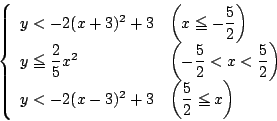
![]() と
と
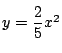 は
は
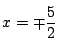 で接し,
で接し,
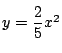 と
と![]() は
は![]() で交わる.また
で交わる.また
![]() と
と![]() は
は![]() で接する.このことに注意して
図示すると右のようになる.
で接する.このことに注意して
図示すると右のようになる.
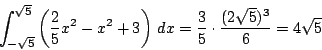 □
□![]() ,
,
![]() とおく.
線分 PQ を1:2に内分する点Rの座標を
とおく.
線分 PQ を1:2に内分する点Rの座標を![]() とする.
このとき,
とする.
このとき,
![]() を消去して
を消去して
 ここで
ここで![]() と領域
と領域![]() ,
,![]() の共有部分が
の共有部分が![]() の変域を与える.
の変域を与える.![]() のとき
のとき
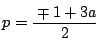 なので,図から
なので,図から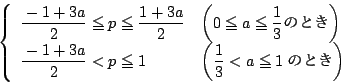
![]() は条件
は条件![]() によってつねに
によってつねに![]() の変域の内にある.
よって
の変域の内にある.
よって![]() の最小値はつねに
の最小値はつねに![]() である.
また
である.
また![]() の変域の中点はそれぞれ
の変域の中点はそれぞれ
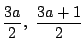 であり,
であり,
![]() はこれより小さいので,最大値は変域の右端でとる.
はこれより小さいので,最大値は変域の右端でとる.
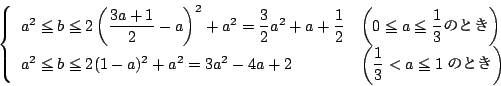
![]() の条件を
の条件を![]() で表すと,
で表すと,
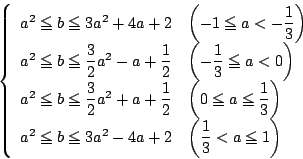
![]() と
と
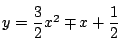 は
は
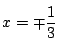 で交わる.また
で交わる.また
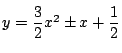 の
の