数学の存在証明においてもこれは大切な問題だ. 例えば「必要条件でしぼる」の例題3.6の十分性の証明を見てほしい.存在に関わる部分だけを取り出すと,
これを証明せよということになる.これは次のように作ってみせた.が奇数または4の倍数なら
には整数解が存在する.
![]() とおく.すると
とおく.すると
ある条件の下で作ってみせることができれば,その条件が存在するための十分条件であることがわかる.構成すること,これが存在証明の基本である.これをまず銘記しよう.
例題 1.16 [04千葉大後期]
直角をはさむ2辺の長さがともに整数の直角三角形を「整直角三角形」という.
二等辺三角形でない二つの整直角三角形を![]() とし,
それぞれの斜辺の長さを
とし,
それぞれの斜辺の長さを![]() とする.
このとき,
これらの積
とする.
このとき,
これらの積![]() を斜辺の長さにもつ整直角三角形が存在することを示せ.
を斜辺の長さにもつ整直角三角形が存在することを示せ.
考え方 これは直接作ってみせることで存在を示す. 問題文中の条件を適切に使っているかよく注意しよう.
解答
![]() が整直角三角形
が整直角三角形![]() の斜辺なので
の斜辺なので
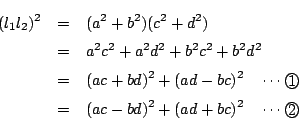
ここで![]() かつ
かつ![]() ならば,
ならば,![]() と
と![]() の辺々をかけて
の辺々をかけて
よって①または②の少なくとも一方は次のことを示している.
0でない二つの整数で,それらの平方の和が![]() の平方に等しいものが存在する.
つまり積
の平方に等しいものが存在する.
つまり積![]() を斜辺の長さにもつ整直角三角形が存在することが示された.
□
を斜辺の長さにもつ整直角三角形が存在することが示された.
□