大阪市には頭髪の本数が同じである二人が少なくとも一組存在する.これを証明せよ.
人間の頭髪がどれくらいあるかはもちろん人によりけりだ.
私なんかは当然少ない方だが,たとえ
![]() 四方に10本とし,頭皮を
四方に10本とし,頭皮を
![]() としても90万本,
これを越えることはない.
大阪市の人口は90万人より多い.
これらの人の頭髪の本数がすべて異なると仮定すれば,
小さい方から並べると最後の人は大阪市の人口より多い頭髪でなければならないが,
それはあり得ない.
ゆえに必ず少なくとも一組,頭髪の本数が同じ人が存在する!
としても90万本,
これを越えることはない.
大阪市の人口は90万人より多い.
これらの人の頭髪の本数がすべて異なると仮定すれば,
小さい方から並べると最後の人は大阪市の人口より多い頭髪でなければならないが,
それはあり得ない.
ゆえに必ず少なくとも一組,頭髪の本数が同じ人が存在する!
これが有限個のもののなかでの存在を保証する「鳩の巣原理」である. 注意すべきは「私と同じ本数の人がいる」は一般には成立しないということだ.だから誰と誰が頭髪の本数が等しいのかはわからないし, それはまた別の問題である.
例題 1.17 [89広島大学]
次の文章は,ある条件を満たすものが存在することを証明する際に,よく使われる 「鳩の巣原理」(または,抽出(ひきだ)し論法ともいう)を説明したものである.
「 ![]() 個のものが,
個のものが, ![]() 個の箱にどのように分配されても,
個の箱にどのように分配されても, ![]() であれば,
2個以上のものが入っている箱が少なくとも一つ存在する」
であれば,
2個以上のものが入っている箱が少なくとも一つ存在する」
この原理を用いて,次の二つの命題が成り立つことを証明せよ.
解答
![]() ,
, ![]() で「鳩の巣原理」を適用すると,四つの小正三角形のうち少なくとも
一つの小正三角形の内部または周上には二つの点がくる.
かつ,点はもとの正三角形の内部に取るのであるから,
いずれの点も小正三角形の頂点には来ない.
で「鳩の巣原理」を適用すると,四つの小正三角形のうち少なくとも
一つの小正三角形の内部または周上には二つの点がくる.
かつ,点はもとの正三角形の内部に取るのであるから,
いずれの点も小正三角形の頂点には来ない.
三角形の内部および周上にある二点間の距離は最大辺の長さを越えない. 従ってその距離は1より小さい.
「三角形の内部および周上にある二点間の距離は最大辺の長さを越えない」 が明かでない人はさらに考えておこう. 二点 P, Q が三角形の内部にあれば直線PQと三角形の辺の交点をR, Sとする. RやSが頂点でなければRを固定しSを辺上で動かすと,Sが一方の方向に動くときRSは増加する. ゆえにSが頂点に来たときの方が長い.Rについても同様.
この論法は大変重要なものなのでいくつか演習にあげておいた.歴史上もっとも有名なものは
次の定理の証明である.
定理 2
![]() を与えられた無理数とする.このとき
を与えられた無理数とする.このとき
解説 この証明は『数論初歩』「ペル方程式の解の存在」[実数の近似定理]にある. それは単独で理解できることなのでぜひよく味わっておいてほしい. この定理はディリクレの定理といわれ, 整数問題で鳩の巣原理がもっとも本格的に用いられる. この定理にちなんで鳩の巣原理による論法のことを「ディリクレ論法」ともいう.
証明
実数 ![]() に対して
に対して ![]() を含み
を含み ![]() を含まない区間を
を含まない区間を
![]() と表す.
区間
と表す.
区間 ![]() を次のように
を次のように ![]() 等分する.
等分する.
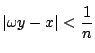 となる
となる
もし有限個しかなかったとする.
そのなかで ![]() の値が最小のもの
を
の値が最小のもの
を
![]() とする.それに対して,
とする.それに対して,
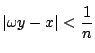 と
なるように
と
なるように
よって相異なるものは無数にある.
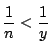 なので
なので
鳩の巣原理は次の形で用いることもある.
整数はすべて
を満たし,さらにすべて異なる.このとき,
は
の値を一回ずつとる.
なぜなら,もし
![]() のなかに,
のなかに,
![]() でとらない値があったとする.
その値を除く数を記した箱を用意する.箱の数は
でとらない値があったとする.
その値を除く数を記した箱を用意する.箱の数は ![]() 個以下になる.
数
個以下になる.
数
![]() をその値にしたがってこれらの箱に入れる.
鳩の巣原理によって
同じ箱に入るものが少なくとも一組できる.
これは
をその値にしたがってこれらの箱に入れる.
鳩の巣原理によって
同じ箱に入るものが少なくとも一組できる.
これは
![]() の値が
すべて異なることに矛盾する.
ゆえに
の値が
すべて異なることに矛盾する.
ゆえに
![]() は
は![]() の値を一回ずつとる.
の値を一回ずつとる.
鳩の巣論法はこの形で一次不定方程式の解の存在の証明に用いられる.
例題 1.18 [00大阪女子大]
以下, ![]() は互いに素な整数とする.
は互いに素な整数とする.
考え方 この4. で鳩の巣原理が用いられる.そのことを念頭において,ぜひいちど自分で考えてほしい.
解答
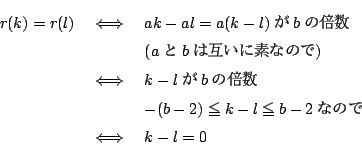
一方 ![]() ならば
ならば ![]() なので
なので
![]() はすべて異なる
はすべて異なる ![]() 個の整数で,すべて
個の整数で,すべて
![]() をみたす.
をみたす.
ゆえに鳩の巣原理により
![]() は
は
![]() の各値を一つずつとる.
ゆえに
の各値を一つずつとる.
ゆえに![]() となる
となる
![]() が存在する.
つまり
が存在する.
つまり![]() が
が ![]() の倍数である.これを
の倍数である.これを ![]() とおくと
とおくと