

 次: 離散的写像の不動点定理
上: 存在の証明
前: 存在の間接証明−鳩の巣論法
次: 離散的写像の不動点定理
上: 存在の証明
前: 存在の間接証明−鳩の巣論法
さらにまた高校数学でやや高度な論証に用いられるのが
「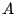 を自然数の部分集合とする.
を自然数の部分集合とする. 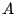 には最小の要素が存在する.」という事実である.
これは自然数の性質に基づくものであり,数学的帰納法の根拠となるものであった.
には最小の要素が存在する.」という事実である.
これは自然数の性質に基づくものであり,数学的帰納法の根拠となるものであった.
自然数の部分集合に最小の要素が存在すること自体は証明なしに使ってもよい.
その例は先にあげた一次不定方程式の整数解の存在定理の別証明だ.
例題1.18の(4)は次のように(3)を用いず直接に示すことができる.
と置く. 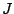 は整数の集合の部分集合であり,
は整数の集合の部分集合であり,
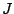 の要素のうち正のもの全体は自然数の集合の部分集合であるから,
の要素のうち正のもの全体は自然数の集合の部分集合であるから,
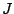 の要素のなかで正で最小のものが存在する.
それを
の要素のなかで正で最小のものが存在する.
それを 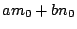 とする.
とする.
このとき,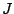 の任意の要素
の任意の要素 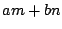 は
は 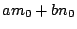 の倍数であることを示す.
の倍数であることを示す.
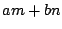 を
を 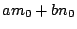 で割り, その除法の式を
で割り, その除法の式を
とする. ただし,
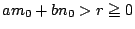 である.
である.
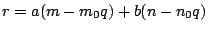 であるから,
であるから,
ここでもし 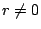 なら
なら 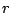 が
が 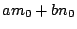 より小さい
より小さい 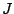 の正の要素になる.
これは
の正の要素になる.
これは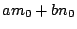 が正で最小の要素であることに反する.ゆえに
が正で最小の要素であることに反する.ゆえに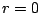 でなければならない.
つまり,
でなければならない.
つまり, 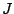 の要素はすべて
の要素はすべて 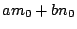 の倍数である.
ところで,
の倍数である.
ところで,
であるから, 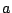 も
も 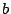 も
も 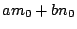 の倍数である.
ところが,
の倍数である.
ところが, 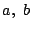 は互いに素であるから,
は互いに素であるから,
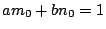 でなければならない.
つまり
でなければならない.
つまり 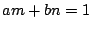 に整数解
に整数解
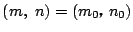 が存在した.
□
が存在した.
□
このように 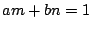 に整数解 が存在することが二つの方法で示された.
実はさらに
に整数解 が存在することが二つの方法で示された.
実はさらに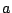 や
や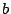 についての数学的帰納法でも可能である.
それはぜひ試みてほしい.
についての数学的帰納法でも可能である.
それはぜひ試みてほしい.
Aozora Gakuen
![]() の任意の要素
の任意の要素 ![]() は
は ![]() の倍数であることを示す.
の倍数であることを示す.
![]() を
を ![]() で割り, その除法の式を
で割り, その除法の式を
![]() に整数解 が存在することが二つの方法で示された.
実はさらに
に整数解 が存在することが二つの方法で示された.
実はさらに![]() や
や![]() についての数学的帰納法でも可能である.
それはぜひ試みてほしい.
についての数学的帰納法でも可能である.
それはぜひ試みてほしい.