自然数 ![]() に対して,1から
に対して,1から ![]() までのすべての自然数の集合を
までのすべての自然数の集合を ![]() とする.
とする.
![]() から
から ![]() への写像
への写像 ![]() が次の条件
が次の条件
をみたすとき,
ただし,集合![]() の各要素に対して集合
の各要素に対して集合![]() の要素を1つずつ対応させる規則のことを,
の要素を1つずつ対応させる規則のことを,
![]() から
から![]() への写像という.
写像は
への写像という.
写像は![]() などで表し,
などで表し,![]() の要素
の要素 ![]() に写像
に写像 ![]() で対応する
で対応する ![]() の要素を
の要素を![]() と書く.
と書く.
例題 1.19 [92神戸大]
自然数 ![]() に対して,1から
に対して,1から ![]() までのすべての自然数の集合を
までのすべての自然数の集合を ![]() とする.
とする.
![]() から
から ![]() への写像
への写像 ![]() が次の条件
が次の条件
ただし,集合![]() の各要素に対して集合
の各要素に対して集合![]() の要素を1つずつ対応させる規則のことを,
の要素を1つずつ対応させる規則のことを,
![]() から
から![]() への写像という.
写像は
への写像という.
写像は![]() などで表し,
などで表し,![]() の要素
の要素 ![]() に写像
に写像 ![]() で対応する
で対応する ![]() の要素を
の要素を![]() と書く.
と書く.
解答 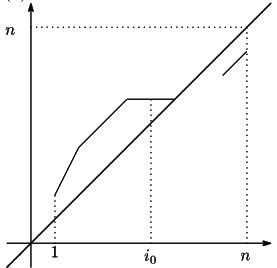
![]() である.
である.
![]() なら
なら ![]() として
として![]() をとればよい.そこで
をとればよい.そこで![]() とする.
とする.
![]() なら
なら ![]() として
として![]() をとればよい.そこで
をとればよい.そこで![]() とする.
とする.
このとき,![]() かつ
かつ ![]() なので
なので ![]() となる
となる ![]() の中の最大のものが存在する.
それを
の中の最大のものが存在する.
それを ![]() とする.
とする.![]() である.
である.
![]() は
は ![]() を満たさないので
を満たさないので
![]() .
.
ところが![]() ならば,つねに
ならば,つねに![]() なので
なので
ここでもし
![]() なら,隣りあう二つの自然数
なら,隣りあう二つの自然数 ![]() と
と ![]() の間にさらに自然数が存在し不合理.
の間にさらに自然数が存在し不合理.
次のような別解もある.
背理法でやってみようとするのは自然な発想だ.
問題をその次の段階.数学的帰納法で![]() を示せれば,
を示せれば,![]() のところで矛盾が起こる.
のところで矛盾が起こる.
別解 背理法で示す.
![]() のすべての
のすべての ![]() に対して
に対して ![]() であるとする.
このときすべての
であるとする.
このときすべての ![]() について
について ![]() であることを数学的帰納法で示す.
であることを数学的帰納法で示す.
![]() かつ
かつ![]() なので
なので ![]() .
.
![]() とする.
とする.![]() ならば,つねに
ならば,つねに![]() なので
なので
![]() .
したがって
.
したがって ![]() であるが
であるが ![]() なので
なので ![]() である.
数学的帰納法によってすべての
である.
数学的帰納法によってすべての ![]() について
について ![]() となる.
となる.
ところがこのとき![]() なので,
なので, ![]() が
が ![]() から
から ![]() への写像であることと矛盾した.
ゆえに
への写像であることと矛盾した.
ゆえに
![]() のの中に少なくとも一つ
のの中に少なくとも一つ![]() となる
となる ![]() が存在する.□
が存在する.□