次: 積分の方法
上: 微分の方法
前: 高次微分
次: 積分の方法
上: 微分の方法
前: 高次微分
平均値の定理を第 次導関数の場合に一般化することで,
関数の展開定理の基礎となるテーラーの定理が得られる.
次導関数の場合に一般化することで,
関数の展開定理の基礎となるテーラーの定理が得られる.
定理 43 (テーラーの定理)
関数

を区間
![$[a,\ b]$](images/img797.gif)
で連続,区間

で

回微分可能な関数とする.
このとき,次のような

が存在する.
証明
とする.ここで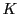 は
は
で定める.すると
よって,
ロルの定理37により,
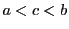 の範囲の
の範囲の で,
で,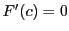 となるものが存在する.
ここで
となるものが存在する.
ここで
であるから,
が成り立つ.つまり
である.よって
である.
□
この証明は平均値の定理とまったく同様である.
つまり,適切な関数 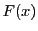 をとりロルの定理から
をとりロルの定理から の存在を示している.
の存在を示している.
関数  を区間
を区間 で
で 回微分可能な関数とする.
区間に属する
回微分可能な関数とする.
区間に属する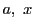 に対し,テーラーの定理(定理43)から
に対し,テーラーの定理(定理43)から
 と
と の間の
の間の を用いて
を用いて
と展開される.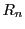 のことを剰余項という.
ここで
のことを剰余項という.
ここで およびその高次導関数がすべて
およびその高次導関数がすべて で有界:
で有界:
であれば,
となる.これは,
関数 を
を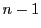 次多項式
次多項式
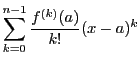 で近似すると,
誤差が
で近似すると,
誤差が
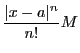 で評価されることを意味している.
さらに定理43を
で評価されることを意味している.
さらに定理43を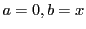 で用い,
で用い,
 を
を
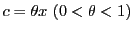 と表すと次のようになる.
と表すと次のようになる.
平均値の定理を 次導関数にまで拡張することで,テーラーの展開定理が得られた.これを1章3節5小節の「関数列の収束」と結びつけることで,関数の級数展開定理が得られる.
次導関数にまで拡張することで,テーラーの展開定理が得られた.これを1章3節5小節の「関数列の収束」と結びつけることで,関数の級数展開定理が得られる.
系 43.1

を区間

で無限回微分可能な関数とし,
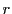
を
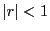
の範囲の定数とする.
であれば,
と展開され,この級数は閉区間
![$[a-r,\ a+r]\subset I$](images/img1353.gif)
で一様収束である.
■
証明
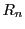 を剰余項とする展開
を剰余項とする展開
で
他の項も
である.ダランベールの判定法系22.2によって正項級数
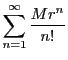 は収束する.
したがって1章3節5小節系31.1により,
本結論が従う.
□
は収束する.
したがって1章3節5小節系31.1により,
本結論が従う.
□
この級数をテーラー級数という.また関数 のこの展開を
テーラー展開という.
のこの展開を
テーラー展開という.
特に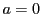 にとった
にとった
をマクローリンの公式,
マクローリン級数という.
例 4.4
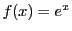
のとき.
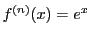
であるから
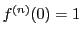
.
また
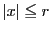
のとき
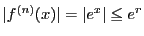
なので
任意の
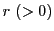
に対する区間
![$[-r,\ r]$](images/img1364.gif)
で
と展開される.収束半径は
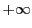
である.
例 4.5
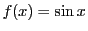
のとき.
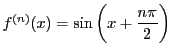
であるから
また
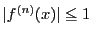
なので
任意の
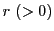
に対する区間
![$[-r,\ r]$](images/img1364.gif)
で
収束半径は
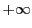
である.
例 4.6 (一般二項展開)
実数

に対し
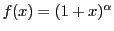
とする.
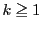
に対して,
したがって,

が自然数

の場合,最終項は
また,
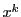
の係数はちょうど
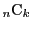
となっているので
となる.これは二項定理そのものである.

が自然数でない場合,剰余項の評価は簡単ではない.
しかし,
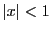
なら
ここで
とする.これを
一般二項展開という.
ここでは数列 の添え字
の添え字 を0を含めた自然数にとる.自然数に0を含めた集合を
を0を含めた自然数にとる.自然数に0を含めた集合を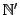 と表した.
と表した.
関数の級数展開とは逆に,級数の形が与えられたとき,それが関数を定める条件を考えよう.
次の定理が数列の収束と関数列の収束を結びつける.
定理 44
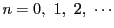
に対する実数列

がある.
関数列
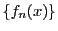
を
で定める.
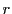
を0でない実数とする.
数列
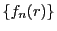
が収束するとき,
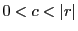
となる

をとると閉区間
![$I=[-c,\ c]$](images/img1385.gif)
で関数列
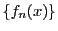
は一様収束し,
開区間
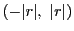
で収束する.
■
証明
級数
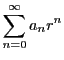 が収束しているので
が収束しているので
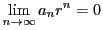 である.
したがって数列
である.
したがって数列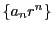 は有界である.
は有界である.
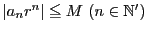 とする.
とする.
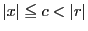 の
の に対して
に対して
となる.
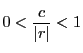 なので
正項級数
なので
正項級数
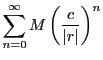 は収束する.系31.1によって
巾級数
は収束する.系31.1によって
巾級数
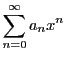 は
は
![$I=[-c,\ c]$](images/img1385.gif) で一様収束する.
開区間
で一様収束する.
開区間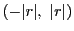 の
の に対し,
に対し,
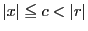 となる
となる をとり,
をとり, を含む閉区間
を含む閉区間![$[-c,\ c]$](images/img1395.gif) に対して前半を用いると
に対して前半を用いると で収束するがわかる.
□
で収束するがわかる.
□
本定理の対偶として次の系が成り立つ.
系 44.1
級数
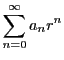
が発散すれば,
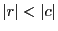
なるすべての

で級数
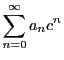
は発散する.
■
級数
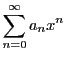 に対し,
に対し,
 に
に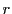 を代入したとき級数が収束するような
を代入したとき級数が収束するような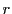 の集合を
の集合を とする.
とする.
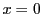 のときは
のときは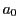 に収束するので,
に収束するので, は空ではない.
は空ではない.
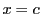 のとき
のとき
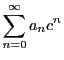 が発散するような
が発散するような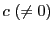 が存在するとする.
すると
が存在するとする.
すると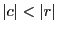 なる
なる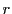 では
発散するのであるから集合
では
発散するのであるから集合 は有界である.
したがってまた
は有界である.
したがってまた の要素の絶対値の集合も有界で,上限が存在する.
この上限を
の要素の絶対値の集合も有界で,上限が存在する.
この上限を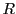 とする.
とする.
また発散するような0でない が存在しないとき,
つまり
が存在しないとき,
つまり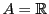 のときは
のときは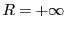 とする.
このとき定理44は次のように述べられる.
とする.
このとき定理44は次のように述べられる.
巾級数
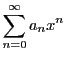 は
開区間
は
開区間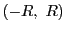 の各点で絶対収束し,
の各点で絶対収束し,
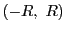 に含まれる任意の閉区間で一様収束する.
に含まれる任意の閉区間で一様収束する.
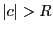 のとき級数
のとき級数
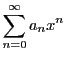 は発散する.
は発散する.
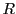 のことを級数
のことを級数
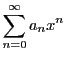 の
収束半径という.
巾級数
の
収束半径という.
巾級数
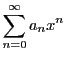 は区間
は区間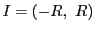 では一つの関数を定めている.
では一つの関数を定めている. に含まれる任意の閉区間での収束は一様なので,その関数は連続である.
巾級数で定まる関数を(実)解析関数という.
に含まれる任意の閉区間での収束は一様なので,その関数は連続である.
巾級数で定まる関数を(実)解析関数という.
系 44.2
巾級数
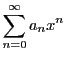
において,
数列
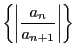
が
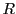
に収束すれば,
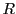
は巾級数の収束半径である.
■
証明
巾級数
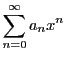 に
に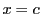 を代入した
級数
を代入した
級数
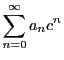 において,
において,
であるから,ダランベールの判定法(系22.2)によって
級数
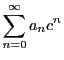 は
は
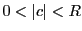 のとき絶対収束し,
のとき絶対収束し,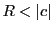 のときは収束しない.
□
のときは収束しない.
□
系 44.3
二つの巾級数
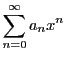
と
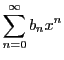
の収束半径がともに
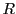
のとき,
二つの巾級数
はともに収束半径
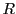
をもち,
である.
■
証明
これは1章2節6小節の定理24の結果である.
□
定理 45 (アーベルの定理)
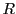
を収束半径とする巾級数
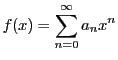
がある.
右辺の級数が
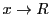
で収束すれば,
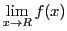
も収束し
である.
■
証明
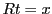 とし
とし
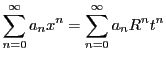 を
を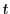 の巾級数とすれば,その収束半径は1で,
の巾級数とすれば,その収束半径は1で,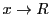 のとき
のとき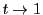 である.
よってはじめから
である.
よってはじめから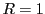 とし,
とし,
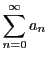 が収束するとき,
が収束するとき,
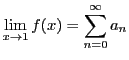 を示せばよい.
を示せばよい.
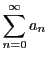 が収束するので
任意の正数
が収束するので
任意の正数 に対して
に対して で
で
となるものが存在する.
このとき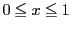 に対して
に対して
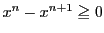 であるから
であるから
ゆえに
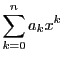 はコーシー列となり一様収束する.
その結果
はコーシー列となり一様収束する.
その結果
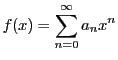 は連続.
は連続.
が成り立つ.
□
多項式関数
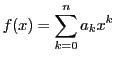 の導関数
の導関数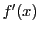 は各項の微分の和
は各項の微分の和
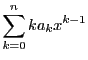 に一致する.
これと同様に巾級数においても,一様収束のもとでは項別微分が可能である.
証明
に一致する.
これと同様に巾級数においても,一様収束のもとでは項別微分が可能である.
証明
1.  を
を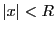 にとり,
にとり,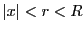 なる
なる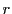 をとる.
をとる.
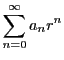 は収束するので
は収束するので
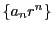 は有界である.
は有界である.
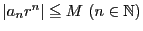 とする.
とする.
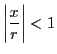 なので
級数
なので
級数
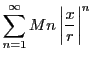 は
収束する.よって
は
収束する.よって
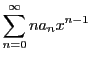 は絶対収束し,収束半径をもつ.それを
は絶対収束し,収束半径をもつ.それを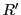 とすると,
とすると,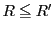 である.
である.
次に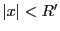 とする.
このとき
とする.
このとき
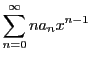 は絶対収束するので
は絶対収束するので
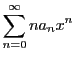 も絶対収束する.
も絶対収束する.
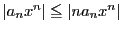 であるから
であるから
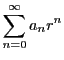 も絶対収束する.
これから
も絶対収束する.
これから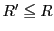 となり,あわせて
となり,あわせて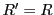 が示された.
が示された.
2.
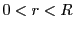 とする.
とする.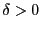 を
を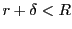 であるようにとる.
そのうえで
であるようにとる.
そのうえで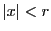 であるような
であるような の値,および
の値,および
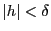 であるような
であるような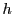 の値を考える.
の値を考える.
 の導関数の定義にしたがって
の導関数の定義にしたがって
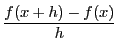 を考えるが,
そのために分子を評価する.
を考えるが,
そのために分子を評価する.
平均値の定理から と
と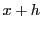 の間の数
の間の数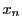 が存在して,
が存在して,
と書ける.よって
次にこれを用いて
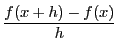 と
と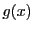 との差を評価する.
との差を評価する.
ここで再び平均値の定理を用いる.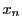 と
と の間の数
の間の数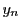 が存在して
が存在して
である.
ここで、
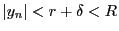 ,
,
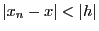 である.
したがって
である.
したがって
1.を2回適用すれば,
 を2回微分して得られるべき級数の収束半径も
を2回微分して得られるべき級数の収束半径も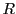 なので,右辺の
なので,右辺の
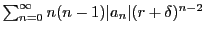 も有限値に収束する.
その値と
も有限値に収束する.
その値と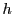 は関係しない.したがって
は関係しない.したがって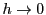 のとき,
右辺も0に収束する.つまり
のとき,
右辺も0に収束する.つまり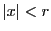 であるすべての
であるすべての に対し,
それを固定するごとに
に対し,
それを固定するごとに は
は において微分可能で,
その微分係数が
において微分可能で,
その微分係数が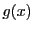 に等しいことが示された.
つまり
に等しいことが示された.
つまり は
は の関数として微分可能で,
その導関数は
の関数として微分可能で,
その導関数は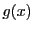 である.
□
である.
□
本定理をくりかえし用いることによりつぎの系が得られる.
系 46.1
巾級数
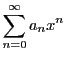
の
収束半径が
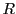
であり,この巾級数によって定まる関数を

とすると,

は無限回微分可能で
である.
■
関数列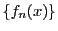 の収束と微分可能性の関係はやや複雑である.
の収束と微分可能性の関係はやや複雑である.
定理 47
開区間
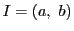
で定義された関数列
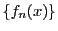
がある.
各

に対して関数
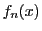
は

で微分可能であり,
かつ関数

に一様収束する.
さらに導関数の列
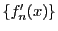
が関数
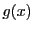
に一様収束するとする.
このとき,関数

も微分可能でその導関数は
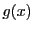
に一致する.
■
証明
区間内の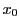 と任意の正数
と任意の正数 が与えられたとする.
が与えられたとする.
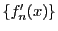 は一様収束するので整数
は一様収束するので整数 で,
で,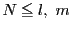 ならば
ならば
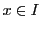 に対して
に対して
となるものが存在する.
次に関数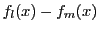 に
に と
と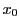 ではさまれた区間で平均値の定理を用いることにより
ではさまれた区間で平均値の定理を用いることにより
となる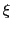 が存在する.
が存在する.
なので
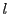 は
は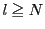 であればよいので
であればよいので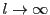 とすることにより,
とすることにより,
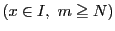 のとき
のとき
が成り立つ.
また導関数の定義から
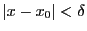 なら
なら
となる正数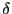 が存在する.
が存在する.
以上から
区間内の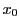 と任意の正数
と任意の正数 に対して,
正数
に対して,
正数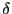 で
で
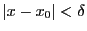 なら
なら
となるものが存在することが示せたので定理が証明された.
□
注意 4.5
導関数列の一様収束性が必要である.
例えば
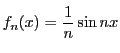
とすると,
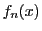
は0に一様収束するが,
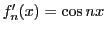
であるから
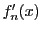
は収束しない.
関数 をより簡単な関数で近似することができないか.
をより簡単な関数で近似することができないか.
この問題に が
が 回微分可能でそれら高次導関数がすべて
回微分可能でそれら高次導関数がすべて で有界:
で有界:
であるならば,テーラー展開がそれに対する解答であった.
関数 を
を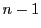 次多項式
次多項式
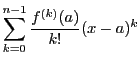 で近似すると,誤差が
で近似すると,誤差が
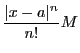 で評価されるのだった.
で評価されるのだった.
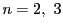 のときは,一次近似,二次近似という.
のときは,一次近似,二次近似という.
一次近似は日常的に用いている.時速30km といえばある時刻での速度によってその運動の時速を近似していることになる.塩水のある一点でからいといえば,その辛さが塩水の辛さと考えている.このようにある点での傾向,傾きをもって全体の傾向,傾きと考えるのは,まさに一次近似である.
逆にいえば内包量を外延量の比で考えることは一次近似を考えていることに過ぎないことがわかる.内包量が微分を考えてはじめて量として十全に把握されることも理解できる.
近似式は
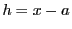 とおくことで実用的な近似式となる.
とおくことで実用的な近似式となる.
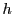 が十分小さいとき
が十分小さいとき
グラフで見ると,一次近似は関数のグラフを接線で近似し,
二次近似は関数のグラフを放物線で近似することになる.
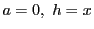 とおいていくつかの関数の近似式を書いてみる.
とおいていくつかの関数の近似式を書いてみる.
このように 回微分可能な関数は
回微分可能な関数は 次式による近似ができ,
その誤差も評価できる.ただこの近似は一点の周りの近似であって,
ある区間での近似ではない.これはいわば関数値の近似である.
次式による近似ができ,
その誤差も評価できる.ただこの近似は一点の周りの近似であって,
ある区間での近似ではない.これはいわば関数値の近似である.
これに対して,ある閉区間で定義された連続関数を,
多項式でその区間で一様に近似することができる.
これは「ワイエルシュトラスの定理」といわれる.
この定理は,フーリエ級数論にもとづくより深い証明があるのだが,
ここではベルンシュタイン(Bernstein)による初等的な証明を紹介する.
まず二項定理に関する補題を示す.
証明
二項定理
に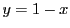 を代入することで 1)を得る.
この等式を
を代入することで 1)を得る.
この等式を で微分し両辺に
で微分し両辺に を乗ずる.
を乗ずる.
を得る.ここに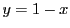 を代入することで 2)を得る.
二項定理の等式を2回微分し
を代入することで 2)を得る.
二項定理の等式を2回微分し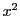 を乗ずる.
を乗ずる.
を得る.ここに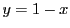 を代入することで 3)を得る.
4)は 2)と 3)を加えて得られる.
□
を代入することで 3)を得る.
4)は 2)と 3)を加えて得られる.
□
定理 48
閉区間
![$[0,\ 1]$](images/img1498.gif)
で連続な関数に対し,

次多項式
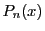
を
で定める.多項式列
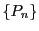
は閉区間
![$[0,\ 1]$](images/img1498.gif)
で一様に収束する.
■
証明
 は閉区間で連続であるから,有界で一様連続である.
つまり,
は閉区間で連続であるから,有界で一様連続である.
つまり,
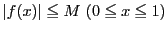 となる
となる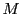 があり,
また任意の正の実数
があり,
また任意の正の実数 に対して,正の数
に対して,正の数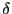 で,
で,
となるものが存在する.
補題の等式1)から
なので,
添え字
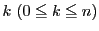 を二つに分ける.
を二つに分ける.
とする.
である.それぞれの和を評価する.
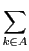 については一様連続性から
については一様連続性から
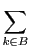 については,有界性から
については,有界性から
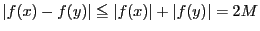 なので
なので
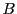 の
の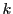 に対しては
に対しては
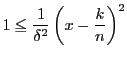 であるから
であるから
したがって
ここで
よって,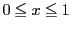 なので
なので
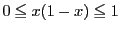 を用いると
を用いると
である.
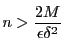 の
の をとると
をとると
である.よって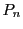 は
は に一様収束する.
□
に一様収束する.
□
系 48.1
閉区間
![$[a,\ b]$](images/img797.gif)
で連続な関数

は多項式で一様に近似される.
■
証明
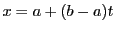 とおく.
とおく.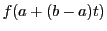 は閉区間
は閉区間![$[0,\ 1]$](images/img1498.gif) で連続である.
定理48より多項式列
で連続である.
定理48より多項式列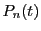 で
で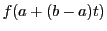 に一様収束するものがある.
に一様収束するものがある.
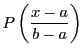 は
は に一様収束する.
□
に一様収束する.
□
例 4.7
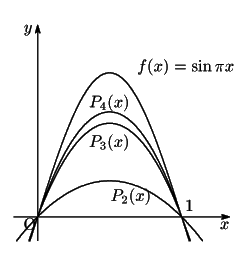
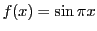
は区間
![$[0,\ 1]$](images/img1498.gif)
でどのように近似されるのか見てみよう.


 次: 積分の方法
上: 微分の方法
前: 高次微分
次: 積分の方法
上: 微分の方法
前: 高次微分
2014-05-23
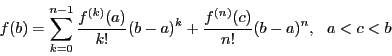
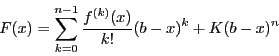
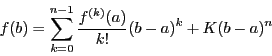
![\begin{displaymath}
F'(x)=
\sum^{n-1}_{k=0}
\left[\dfrac{f^{(k+1)}(x)}{k!}(b-x)^k-\dfrac{f^{(k)}(x)}{k!}k(b-x)^{k-1}
\right]
-Kn(b-x)^{n-1}
\end{displaymath}](images/img1337.gif)
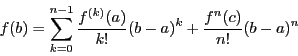
![]() をとりロルの定理から
をとりロルの定理から![]() の存在を示している.
の存在を示している.
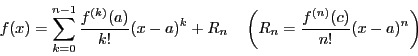
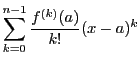 で近似すると,
誤差が
で近似すると,
誤差が
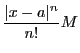 で評価されることを意味している.
さらに定理43を
で評価されることを意味している.
さらに定理43を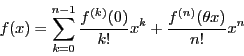
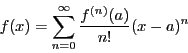
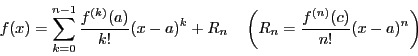
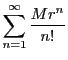 は収束する.
したがって1章3節5小節系31.1により,
本結論が従う.
□
は収束する.
したがって1章3節5小節系31.1により,
本結論が従う.
□
![]() のこの展開を
テーラー展開という.
のこの展開を
テーラー展開という.
![]() にとった
にとった
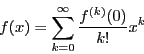
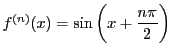 であるから
であるから
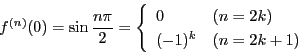
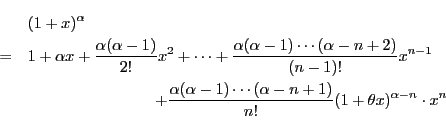
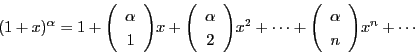
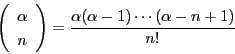
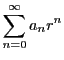 が収束しているので
が収束しているので
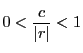 なので
正項級数
なので
正項級数
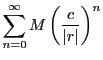 は収束する.系31.1によって
巾級数
は収束する.系31.1によって
巾級数
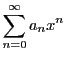 は
は
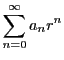 が発散すれば,
が発散すれば,
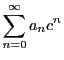 は発散する.
■
は発散する.
■
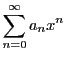 に対し,
に対し,
![]() に
に![]() を代入したとき級数が収束するような
を代入したとき級数が収束するような![]() の集合を
の集合を![]() とする.
とする.
![]() のときは
のときは![]() に収束するので,
に収束するので,![]() は空ではない.
は空ではない.
![]() のとき
のとき
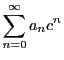 が発散するような
が発散するような![]() が存在するとする.
すると
が存在するとする.
すると![]() なる
なる![]() では
発散するのであるから集合
では
発散するのであるから集合![]() は有界である.
したがってまた
は有界である.
したがってまた![]() の要素の絶対値の集合も有界で,上限が存在する.
この上限を
の要素の絶対値の集合も有界で,上限が存在する.
この上限を![]() とする.
とする.
は 開区間
の各点で絶対収束し,
に含まれる任意の閉区間で一様収束する.
のとき級数
は発散する.
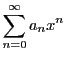 の
収束半径という.
巾級数
の
収束半径という.
巾級数
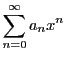 は区間
は区間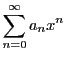 において,
数列
において,
数列
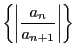 が
が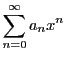 に
に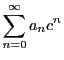 において,
において,
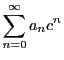 は
は
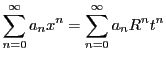 を
を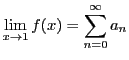 を示せばよい.
を示せばよい.
![]() が収束するので
任意の正数
が収束するので
任意の正数![]() に対して
に対して![]() で
で
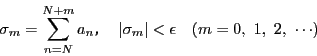
![]() に対して
に対して
![]() であるから
であるから
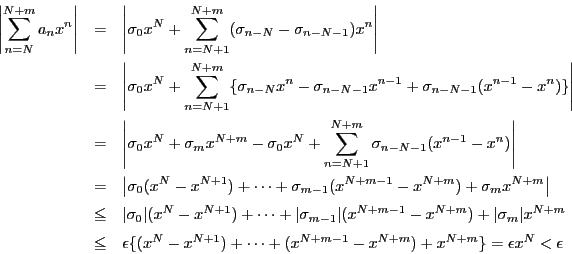
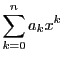 はコーシー列となり一様収束する.
その結果
はコーシー列となり一様収束する.
その結果
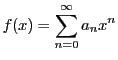 は連続.
は連続.
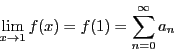
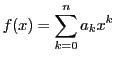 の導関数
の導関数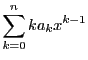 に一致する.
これと同様に巾級数においても,一様収束のもとでは項別微分が可能である.
証明
に一致する.
これと同様に巾級数においても,一様収束のもとでは項別微分が可能である.
証明
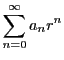 は収束するので
は収束するので
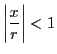 なので
級数
なので
級数
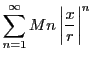 は
収束する.よって
は
収束する.よって
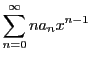 は絶対収束し,収束半径をもつ.それを
は絶対収束し,収束半径をもつ.それを![]() とする.
このとき
とする.
このとき
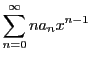 は絶対収束するので
は絶対収束するので
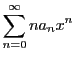 も絶対収束する.
も絶対収束する.
![]() であるから
であるから
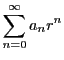 も絶対収束する.
これから
も絶対収束する.
これから![]() となり,あわせて
となり,あわせて![]() が示された.
が示された.
![]() とする.
とする.![]() を
を![]() であるようにとる.
そのうえで
であるようにとる.
そのうえで![]() であるような
であるような![]() の値,および
の値,および
![]() であるような
であるような![]() の値を考える.
の値を考える.
![]() の導関数の定義にしたがって
の導関数の定義にしたがって
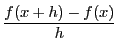 を考えるが,
そのために分子を評価する.
を考えるが,
そのために分子を評価する.
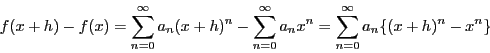
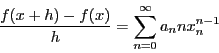
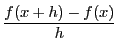 と
と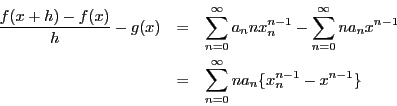
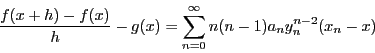
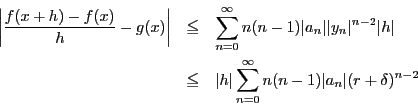
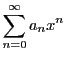 の
収束半径が
の
収束半径が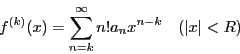
![]() は一様収束するので整数
は一様収束するので整数![]() で,
で,![]() ならば
ならば
![]() に対して
に対して
![]() に
に![]() と
と![]() ではさまれた区間で平均値の定理を用いることにより
ではさまれた区間で平均値の定理を用いることにより
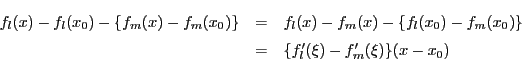
![]() は
は![]() であればよいので
であればよいので![]() とすることにより,
とすることにより,
![]() のとき
のとき
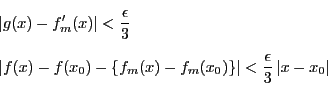
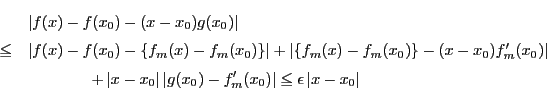
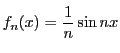 とすると,
とすると,
![]() が
が![]() 回微分可能でそれら高次導関数がすべて
回微分可能でそれら高次導関数がすべて![]() で有界:
で有界:
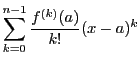 で近似すると,誤差が
で近似すると,誤差が
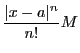 で評価されるのだった.
で評価されるのだった.
![]() とおくことで実用的な近似式となる.
とおくことで実用的な近似式となる.
![]() が十分小さいとき
が十分小さいとき
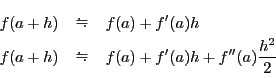
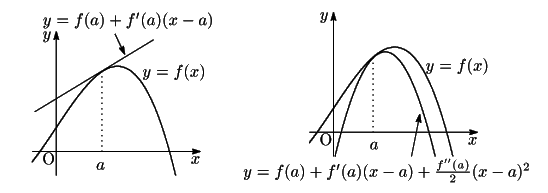
![]() とおいていくつかの関数の近似式を書いてみる.
とおいていくつかの関数の近似式を書いてみる.
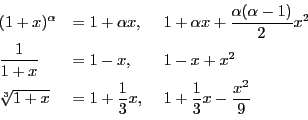
![]() 回微分可能な関数は
回微分可能な関数は![]() 次式による近似ができ,
その誤差も評価できる.ただこの近似は一点の周りの近似であって,
ある区間での近似ではない.これはいわば関数値の近似である.
次式による近似ができ,
その誤差も評価できる.ただこの近似は一点の周りの近似であって,
ある区間での近似ではない.これはいわば関数値の近似である.
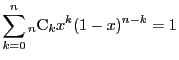
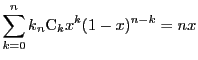
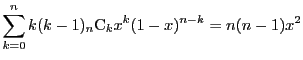
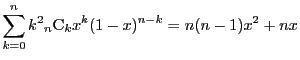
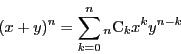
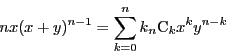
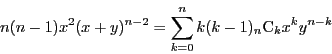
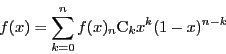
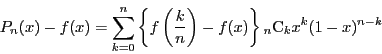
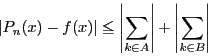
![]() については一様連続性から
については一様連続性から
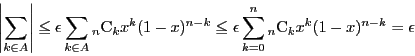
![]() については,有界性から
については,有界性から
![]() なので
なので
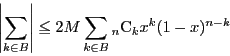
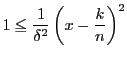 であるから
であるから
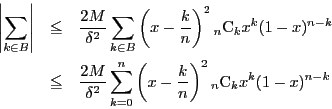
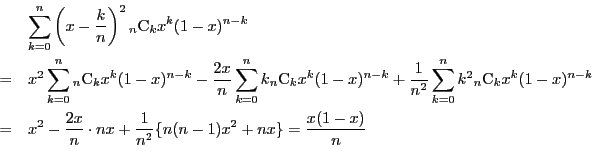
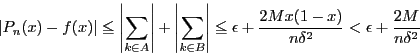
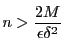 の
の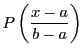 は
は