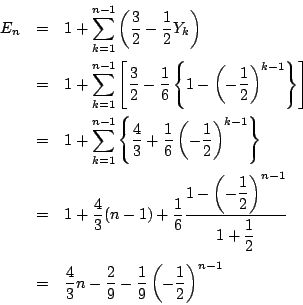東大理系前期6 問題 解説 2001年入試に戻る
n 回の操作の後の点 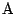 の座標を an ,
点
の座標を an ,
点 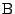 の座標を bn とする.
の座標を bn とする.
-
- (1)
点
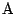 と点
と点 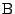 の座標の差は高々1である.
なぜなら,
の座標の差は高々1である.
なぜなら, 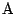 と点
と点 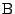 の座標が同じなら
1回の操作で1差が出来る.
の座標が同じなら
1回の操作で1差が出来る.
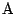 と点
と点  の座標の差が1なら,
差が1のままか同じ座標になるかしかないからである.
an+1=bn+1 となるのは, an=bn-1 で表が出るか,
bn=an-1 で裏が出る場合のみである.
の座標の差が1なら,
差が1のままか同じ座標になるかしかないからである.
an+1=bn+1 となるのは, an=bn-1 で表が出るか,
bn=an-1 で裏が出る場合のみである.
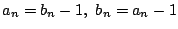 となる場合の数はそれぞれ
となる場合の数はそれぞれ
である.
- (2)
X1=0 である.
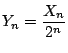 とおくと
(1)より
とおくと
(1)より
これから
- (3)
n回後のaの平均とb の平均は等しい.そこで a+b の平均が求まれば
よいので,n回の試行における2n通りのan+bnの値の平均をEnとおく.
E1=1 より
[別解]
n 回後の a の平均と b の平均は等しい.そこで a+b の平均が求まれば
よいので, n 回の試行における an+bn の期待値を En とおく.
n 回目から次の1回の試行で2増えるのは an<bnで裏が出るか,
bn<an で表が出る場合のみである.したがって
(以下は上と同じ計算)
![]() の座標を an ,
点
の座標を an ,
点 ![]() の座標を bn とする.
の座標を bn とする.
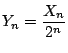 とおくと
(1)より
とおくと
(1)より
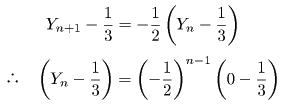
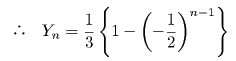
![]()