

 次: 調和列点と対合
上: 射影変換と複比
前: 射影変換と複比
次: 調和列点と対合
上: 射影変換と複比
前: 射影変換と複比
複比を直線の長さから独立に定義する段階に至った.
古典的な複比の概念を含む射影空間の複比を定義し,運用する.
そのために以下において,
係数体 は可換であるとし,さらにその標数は2でないとする.
は可換であるとし,さらにその標数は2でないとする.
射影空間から射影空間への一対一変換のなかで,
何を保存すればそれが射影変換であるといえるのか.
結論としていえば,複比を変えない一対一変換が射影変換なのである.
複比を,長さのような量的概念から独立に定義し,射影幾何の古典的な証明を,新たな基礎のうえに置くこと,これがパスカルの定理のさまざまの証明を反省した結果の要請であった.
これをおこなうと,それによってまた,射影変換を特徴づける量としての
複比が確立する.
 が可換であれば,一つの直線体
が可換であれば,一つの直線体
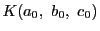 に対する同型
に対する同型
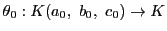 を指定することで,
他の任意の直線体
を指定することで,
他の任意の直線体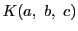 に対して
同型
に対して
同型
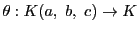 で
で
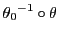 が直線の射影写像となるものが一意に定まる.可換でなければ内部自己同型の自由さがある.
が直線の射影写像となるものが一意に定まる.可換でなければ内部自己同型の自由さがある.
以下では, を可換とし,
すべての直線体にこのような同型
を可換とし,
すべての直線体にこのような同型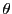 が指定されているもとする.よって,枠
が指定されているもとする.よって,枠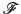 を指定することで
を指定することで 次元射影空間
次元射影空間 の任意の面上の同次座標は,一意に定まる.また
の任意の面上の同次座標は,一意に定まる.また の射影変換は,座標系では
の射影変換は,座標系では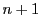 次可逆行列の定数倍による同値類で表される.
次可逆行列の定数倍による同値類で表される.
定義 25

の直線

上の4点
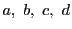
において
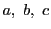
は相異なりかつ
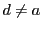
とする.
枠
![$\bigl[b,\ a,\ c\bigr]$](images/img1818.gif)
に関する
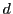
の非同次座標を
この4点の
複比といい,
![$\bigl[a,\ b;\ c,\ d\bigr]$](images/img183.gif)
で表す.
■
複比は言いかえれば直線体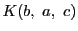 から係数体への同型
から係数体への同型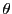 に対する
に対する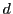 の
の での値
での値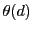 である.
である.
四角性六点という性質が射影変換 で不変であることによって,
射影変換
で不変であることによって,
射影変換 に関して複比は不変である.
つまり
に関して複比は不変である.
つまり
である.
複比を一般の枠に関する同次座標によって具体的に表そう.
直線上に同次座標が定まり,4点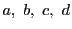 の同次座標が
の同次座標が
であるとする.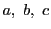 が相異なるので
が相異なるので
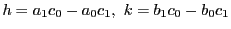 はそれぞれ0でない
はそれぞれ0でない の値である.行列
の値である.行列
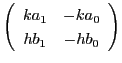 に対応する射影変換で
に対応する射影変換で
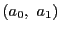 ,
,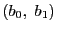 ,
,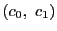 はそれぞれ
はそれぞれ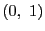 ,
,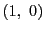 ,
,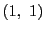 にうつる.この射影変換で
にうつる.この射影変換で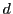 は
は
にうつる.したがって
が
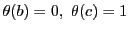 となるように定まっている
となるように定まっている
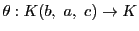 をとると,
をとると,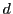 の非同次座標
の非同次座標
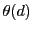 は
は
となる.これを最初に与えられた非同次座標で表そう.
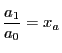 ,
,
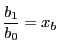 ,
,
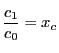 ,
,
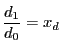 とおくと
とおくと
となり,古典的な複比の定義2と一致する.
先に長さを用いて定義した複比において示した諸性質,
補題4,
補題6,補題7はそのまま成り立つ.
それら再構成し,証明も再度行う.まず補題6.
命題 64
直線上の5点
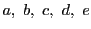
について
なら
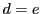
である.
■
証明
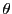 は体の同型であるから.
は体の同型であるから.
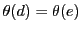 なら
なら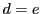 である.
□
である.
□
射影変換は複比を変えないがその逆も成り立つ.
すなわち次の命題が成立する.
命題 65
直線

から直線
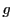
への一対一対応が複比を変えなければ,
それは射影写像である.
■
証明
 から
から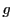 への写像
への写像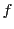 が複比を変えないとする.
が複比を変えないとする.
 の枠
の枠
![$\mathscr{F}=\bigl[b,\ a,\ c\bigr]$](images/img1838.gif) をとり,
をとり,
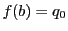 ,
,
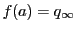 ,
,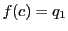 とおく.
命題35によって射影写像
とおく.
命題35によって射影写像 で
で
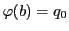 ,
,
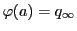 ,
,
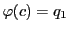 と
なるものが存在する.
と
なるものが存在する.
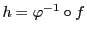 とおく.このとき
とおく.このとき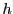 は
は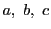 を動かさない.
かつ
を動かさない.
かつ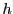 は複比を変えないので,
は複比を変えないので, の任意の点
の任意の点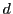 に対して
に対して
が成り立つ.つまり
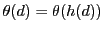 であるが,
であるが,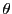 は同型なので
任意の
は同型なので
任意の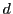 に対し
に対し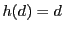 .つまり
.つまり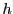 は恒等写像であり,この結果,
は恒等写像であり,この結果,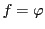 となって,
確かに
となって,
確かに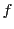 は射影写像である.
□
は射影写像である.
□
射影空間から射影空間への一対一変換のなかで,
複比を変えない変換は射影変換であることが確立した.
これは射影変換の特徴づけであり,
それが複比を射影幾何の公理から再構成することによっておこなわれた.
命題 66
直線

上の4点
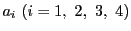
と
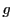
上の4点
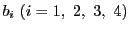
について,
が成り立てば,

から
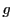
への射影写像

で
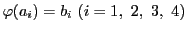
となるものが存在する.
■
証明
命題35により,射影写像 で
で
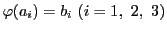 となるものが存在する.
となるものが存在する.
なので,命題64より
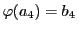 である.
□
である.
□
命題 67
点

を共有する2直線上の点列
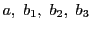
と
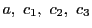
に対して
が成りたてば,3直線
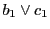
,
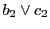
,
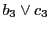
は共点である.
■
証明
命題66により
射影写像 で
で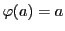 ,
,
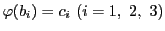 となるものが存在する.
直線体が可換であるから命題48が成立する.
よって
となるものが存在する.
直線体が可換であるから命題48が成立する.
よって は配景写像であり,3直線
は配景写像であり,3直線
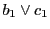 ,
,
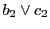 ,
,
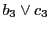 は配景写像の中心で交わる.
□
は配景写像の中心で交わる.
□
射影平面 で考える.
で考える.
 上に1点
上に1点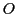 がある.
点
がある.
点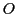 を通る直線の集合を
を通る直線の集合を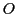 を中心とする線束という.
を中心とする線束という.
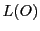 のように書き表す.
のように書き表す.
直線体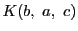 は直線上の3点を基準にして,
その直線上の点に対して体の構造を導入するものであった.
それを可能にする根拠は命題43の
四角性六点性の射影変換での不変性であった.
は直線上の3点を基準にして,
その直線上の点に対して体の構造を導入するものであった.
それを可能にする根拠は命題43の
四角性六点性の射影変換での不変性であった.
同様に,その双対命題として
四辺性六辺性もまた射影変換で不変である.
よって, において線束が与えられると,
線束の3直線
において線束が与えられると,
線束の3直線
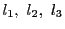 を基準に選び
四辺性六辺を用いて線束に体の構造を入れることが出来る.
これを
を基準に選び
四辺性六辺を用いて線束に体の構造を入れることが出来る.
これを
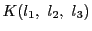 とする.
とする.
定義 26
線束をなす4直線
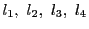
がある.
3直線
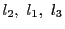
で定まる直線体を
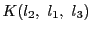
とする.
同型
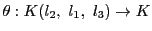
をとる.
4直線
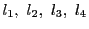
の複比
![$\bigl[l_1,\ l_2;\ l_3,\ l_4\bigr]$](images/img1870.gif)
を値
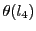
と定める.
■
命題 68

に座標系を導入する.超平面座標によって
点
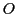
を通る4直線
は
双対空間

上のある直線とその上にある4点に対応する.
この4点で定まる複比を考える.

に座標変換を行うと超平面座標も座標変換を受け,
座標変換は射影変換であるから,この複比は

の座標系のとり方によらない.
これを
![$\bigl[l_1,\ l_2;\ l_3,\ l_4\bigr]_*$](images/img1872.gif)
とおく.
である.
■
証明
 において四角性六点の双対概念としての四辺性六辺とは,
において四角性六点の双対概念としての四辺性六辺とは,
 における四角性六点を,点と直線,含む含まれるの関係を逆にして
における四角性六点を,点と直線,含む含まれるの関係を逆にして
 における基本図形としたものを,
射影空間の同型によって
における基本図形としたものを,
射影空間の同型によって に戻したものに他ならない.
に戻したものに他ならない.
点と直線,含む含まれるの関係を逆にすることで,
6点が四角性六点であることと,
6辺が四辺性六辺であることが同値になる.
よって の3直線によって定まる直線体と
対応する
の3直線によって定まる直線体と
対応する の3点によって定まる直線体は同型であり,
対応する
の3点によって定まる直線体は同型であり,
対応する の直線と
の直線と の点がそれぞれの係数体でとる値は等しい.
□
の点がそれぞれの係数体でとる値は等しい.
□
命題 69

の点
を中心とする線束に属する4直線
がある.
を通らない直線
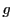
と4直線
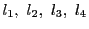
の交点を
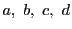
とすれば,
である.
■
証明
命題42によって,
四辺性六辺の直線による切断の交点は四角性六点である.
これはいいかえると
3直線
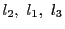 をもとに定義された線束の直線間の和と積による体
をもとに定義された線束の直線間の和と積による体
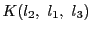 と,
3点
と,
3点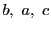 で定義された直線
で定義された直線 上の点の間の和と積による体
上の点の間の和と積による体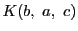 は,
線束の直線と直線
は,
線束の直線と直線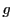 による交点との対応で同型となるということである.
したがって
による交点との対応で同型となるということである.
したがって
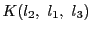 における
における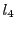 の値と,
の値と,
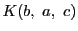 における
における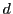 の値は等しい.
つまり
の値は等しい.
つまり
![$\bigl[l_1,\ l_2;\ l_3,\ l_4\bigr]=\bigl[a,\ b;\ c,\ d\bigr]$](images/img1876.gif) である.
□
である.
□
直接計算による証明
 の座標系を定め2直線
の座標系を定め2直線
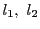 の超平面座標を
の超平面座標を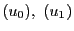 とする.
とする.
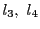 がそれぞれ媒介変数を用いて
がそれぞれ媒介変数を用いて
と表されるとする.点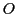 に対応する
に対応する の直線上の同次座標で,
4直線に対応する4点の同次座標が
の直線上の同次座標で,
4直線に対応する4点の同次座標が
であるような座標変換,つまり射影写像が存在する.
よってその複比は
である.
次に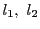 と
と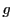 の交点の座標を
の交点の座標を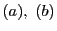 とする.
とする.
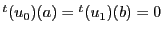 で,
で,
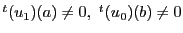 である.
また
である.
また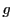 の超平面座標も
の超平面座標も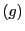 で表す.ここで点
で表す.ここで点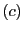 を
を
で定める.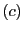 は
は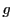 上の点である.一方,
上の点である.一方,
よってこれが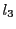 と
と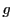 の交点である.
の交点である.
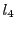 と
と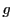 の交点も同様である.
よって直線
の交点も同様である.
よって直線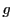 上の同次座標で
上の同次座標で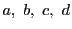 の同次座標が
の同次座標が
となるものがとれる.よってその複比は
となり,命題69が証明された.
□
注意 3.3.1
これから補題
4が従うことに注意しよう.
つまり,値
![$\bigl[a,\ b;\ c,\ d\bigr]$](images/img183.gif)
は直線
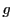
のとり方によらない.
4点の並べ替えは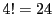 通りあるが,
すでに古典的定義でもみたように,複比の値は次のように4個ずつ等しい.
4点がすべて相異なる場合についてみてみると,値が次のように6通りに変化する.
通りあるが,
すでに古典的定義でもみたように,複比の値は次のように4個ずつ等しい.
4点がすべて相異なる場合についてみてみると,値が次のように6通りに変化する.
とおく.この式から
さらに,
より
である.これらを組みあわせることで
を得る.
これら6個の値は一般的には異なるが,
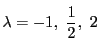 のとき,および
のとき,および
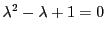 のとき,同じものが現れる.
のとき,同じものが現れる.
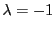 のときは
のときは
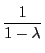 が
が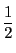 となる.
となる.
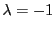 のとき4点
のとき4点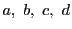 は調和点列をなすという.
は調和点列をなすという.
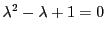 を満たすとき,4点は等非調和列点という.
を満たすとき,4点は等非調和列点という.
また,
![$\bigl[a,\ b;\ c,\ d\bigr]$](images/img183.gif) において,
において,
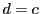 のとき
のとき
![$\bigl[a,\ b;\ c,\ d\bigr]=1$](images/img1899.gif) ,
,
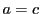 または
または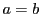 なら
なら
![$\bigl[a,\ b;\ c,\ d\bigr]=0$](images/img1902.gif) ,
,
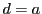 なら
なら
![$\bigl[a,\ b;\ c,\ d\bigr]=\infty$](images/img1904.gif) とし,
とし,
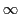 に関する形式的演算を
に関する形式的演算を
と定めれば,
![$\bigl[a,\ b;\ c,\ d\bigr]$](images/img183.gif) は少なくとも3個が異なる場合にすべて定義される.
複比が0,1,
は少なくとも3個が異なる場合にすべて定義される.
複比が0,1,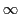 のいずれかになるのは,
4点のいずれか2点が等しい場合にかぎることもただちにわかる.
のいずれかになるのは,
4点のいずれか2点が等しい場合にかぎることもただちにわかる.
ということは,本来複比は次のように定義すべきである.
射影直線 上の少なくとも3個は異なる4点の組の集合
上の少なくとも3個は異なる4点の組の集合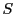 をとる.
をとる.
複比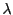 とは,同次座標によって次式で定まる
とは,同次座標によって次式で定まる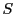 から射影直線
から射影直線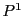 への写像である.
への写像である.
 の射影変換で互いに移りかわる点の組,
および上記入れかえによる4個ずつの組は
この写像で同一の同次座標となる.
の射影変換で互いに移りかわる点の組,
および上記入れかえによる4個ずつの組は
この写像で同一の同次座標となる.
古典的な射影幾何は,点の組や直線の組が,配景写像や射影写像によって対応するかどうかという観点でとらえてきた.基本図形が配景的関係にあるか,射影的関係にあるか,ということである.
しかしそれは複比の相等で記述することができる.
以下において古典的な射影幾何の方法による証明は,
複比の相等による論述で行う.


 次: 調和列点と対合
上: 射影変換と複比
前: 射影変換と複比
2014-01-03
次: 調和列点と対合
上: 射影変換と複比
前: 射影変換と複比
2014-01-03
![]() を可換とし,
すべての直線体にこのような同型
を可換とし,
すべての直線体にこのような同型![]() が指定されているもとする.よって,枠
が指定されているもとする.よって,枠![]() を指定することで
を指定することで![]() 次元射影空間
次元射影空間![]() の任意の面上の同次座標は,一意に定まる.また
の任意の面上の同次座標は,一意に定まる.また![]() の射影変換は,座標系では
の射影変換は,座標系では![]() 次可逆行列の定数倍による同値類で表される.
次可逆行列の定数倍による同値類で表される.
![]() から係数体への同型
から係数体への同型![]() に対する
に対する![]() の
の![]() での値
での値![]() である.
である.
![]() で不変であることによって,
射影変換
で不変であることによって,
射影変換![]() に関して複比は不変である.
つまり
に関して複比は不変である.
つまり
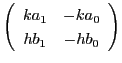 に対応する射影変換で
に対応する射影変換で
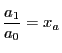 ,
,
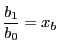 ,
,
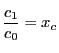 ,
,
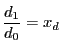 とおくと
とおくと
![]() は直線上の3点を基準にして,
その直線上の点に対して体の構造を導入するものであった.
それを可能にする根拠は命題43の
四角性六点性の射影変換での不変性であった.
は直線上の3点を基準にして,
その直線上の点に対して体の構造を導入するものであった.
それを可能にする根拠は命題43の
四角性六点性の射影変換での不変性であった.
![]() において線束が与えられると,
線束の3直線
において線束が与えられると,
線束の3直線
![]() を基準に選び
四辺性六辺を用いて線束に体の構造を入れることが出来る.
これを
を基準に選び
四辺性六辺を用いて線束に体の構造を入れることが出来る.
これを
![]() とする.
とする.
![]() の3直線によって定まる直線体と
対応する
の3直線によって定まる直線体と
対応する![]() の3点によって定まる直線体は同型であり,
対応する
の3点によって定まる直線体は同型であり,
対応する![]() の直線と
の直線と![]() の点がそれぞれの係数体でとる値は等しい.
□
の点がそれぞれの係数体でとる値は等しい.
□
![]() の座標系を定め2直線
の座標系を定め2直線
![]() の超平面座標を
の超平面座標を![]() とする.
とする.
![]() がそれぞれ媒介変数を用いて
がそれぞれ媒介変数を用いて
![]() と
と![]() の交点の座標を
の交点の座標を![]() とする.
とする.
![]() で,
で,
![]() である.
また
である.
また![]() の超平面座標も
の超平面座標も![]() で表す.ここで点
で表す.ここで点![]() を
を
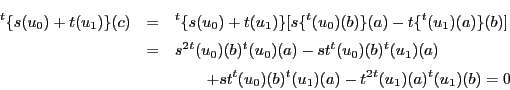
![\begin{eqnarray*}
\lambda&=&
\bigl[a,\ b;\ c,\ d\bigr]=
\bigl[b,\ a;\ d,\ c\b...
...d\bigr]=
\bigl[c,\ d;\ b,\ a\bigr]=
\bigl[d,\ c;\ a,\ b\bigr]
\end{eqnarray*}](images/img1893.gif)
![\begin{eqnarray*}
\bigl[a,\ c;\ b,\ d\bigr]+\bigl[a,\ b;\ c,\ d\bigr]&=&
\dfra...
...-b_1c_0)-a_1d_0(b_0c_1-b_1c_0)}{(a_0d_1-a_1d_0)(b_0c_1-b_1c_0)}=1\end{eqnarray*}](images/img1894.gif)
![\begin{eqnarray*}
\dfrac{1}{1-\lambda}&=&
\bigl[a,\ c;\ d,\ b\bigr]=
\bigl[c,...
...c\bigr]=
\bigl[b,\ c;\ d,\ a\bigr]=
\bigl[c,\ b;\ a,\ d\bigr]
\end{eqnarray*}](images/img1896.gif)
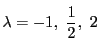 のとき,および
のとき,および
![]() のときは
のときは
![]() が
が![]() となる.
となる.
![]() のとき4点
のとき4点![]() は調和点列をなすという.
は調和点列をなすという.
![]() を満たすとき,4点は等非調和列点という.
を満たすとき,4点は等非調和列点という.
![]() において,
において,
![]() のとき
のとき
![]() ,
,
![]() または
または![]() なら
なら
![]() ,
,
![]() なら
なら
![]() とし,
とし,
![]() に関する形式的演算を
に関する形式的演算を
上の少なくとも3個は異なる4点の組の集合
をとる.
とは,同次座標によって次式で定まる
から射影直線
への写像である.
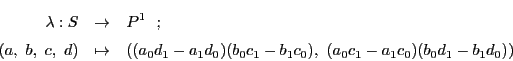
![]() の射影変換で互いに移りかわる点の組,
および上記入れかえによる4個ずつの組は
この写像で同一の同次座標となる.
の射影変換で互いに移りかわる点の組,
および上記入れかえによる4個ずつの組は
この写像で同一の同次座標となる.