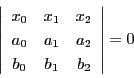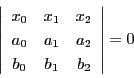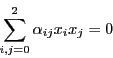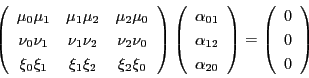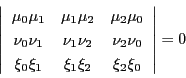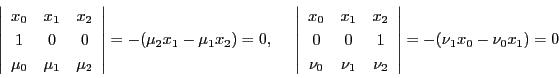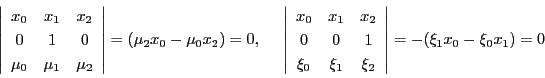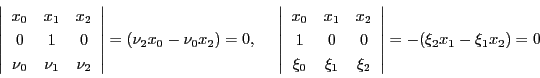次: 代数的な証明
上: パスカルの定理
前: 幾何的定義による証明
次: 代数的な証明
上: パスカルの定理
前: 幾何的定義による証明
次に,座標による定義をもとにした証明をおこなおう.
すでに「重心座標による証明」がある.これを射影幾何での証明に甦らせよう.
 に枠が定まればこれによって同次座標が定まる.
同次座標が
に枠が定まればこれによって同次座標が定まる.
同次座標が
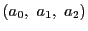 ,
,
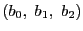 である
二点
である
二点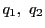 を通る直線の方程式は
を通る直線の方程式は
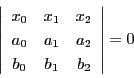 |
(4.3) |
と表される.
なぜなら,直線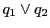 上の点
上の点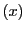 は媒介変数
は媒介変数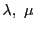 をもちいて
をもちいて
と表される.ただし
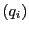 で点
で点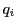 の同次座標を表している.
これは
の同次座標を表している.
これは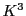 における3ベクトル
における3ベクトル
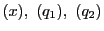 が一次従属であることとで,
それはまた3ベクトルによる行列式が0であることと同値になるからである.
そしてこれは3点
が一次従属であることとで,
それはまた3ベクトルによる行列式が0であることと同値になるからである.
そしてこれは3点
が共線である条件でもある.
 において一般の位置にある4点
において一般の位置にある4点
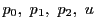 による
枠
による
枠
![$\mathscr{F}=[p_0,\ p_1,\ p_2,\ u]$](images/img2405.gif) によって
同次座標が定まっているとき,
三角形
によって
同次座標が定まっているとき,
三角形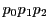 をこの同次座標の座標三角形という.
座標三角形の頂点である3点は,この同次座標に関して
をこの同次座標の座標三角形という.
座標三角形の頂点である3点は,この同次座標に関して
となる.この座標三角形を使えば,重心座標によるパスカルの定理の証明を書き直すことができる.
定理10の3点
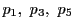 とこれらと一般の位置にある点
とこれらと一般の位置にある点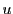 をとり,
枠
をとり,
枠
![$\mathscr{F}=[p_1,\ p_3,\ p_5]$](images/img2408.gif) を定める.
この同次座標による
を定める.
この同次座標による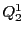 の方程式を
の方程式を
とする.これが
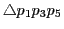 の頂点を通る.
頂点の同次座標
の頂点を通る.
頂点の同次座標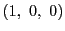 ,
,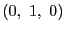 ,
,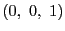 が方程式を満たすので,
が方程式を満たすので,
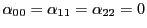 である.
よって方程式は
である.
よって方程式は
となる.
枠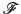 に関する他の3点の座標を
に関する他の3点の座標を
とする.これらが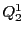 上にあるので
上にあるので
係数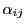 のすべてが0ではないので,
のすべてが0ではないので,
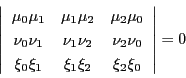 |
(4.4) |
である.
二点
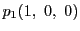 ,
,
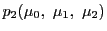 を通る直線の方程式と,
二点
を通る直線の方程式と,
二点
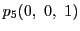 ,
,
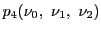 を通る直線の方程式は,それぞれ
を通る直線の方程式は,それぞれ
となる.これより
なので,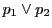 と
と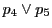 の交点
の交点 の座標は
の座標は
同様にして,
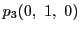 ,
,
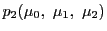 を通る直線の方程式と,
を通る直線の方程式と,
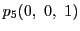 ,
,
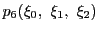 を通る直線の方程式
を通る直線の方程式
から交点 を求めると
を求めると
また
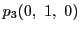 ,
,
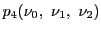 を通る直線の方程式と,
を通る直線の方程式と,
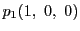 ,
,
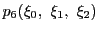 を通る直線の方程式
を通る直線の方程式
から
交点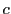 を求めると
を求めると
となる.
つまり3点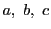 は共線である.
□
は共線である.
□


 次: 代数的な証明
上: パスカルの定理
前: 幾何的定義による証明
2014-01-03
次: 代数的な証明
上: パスカルの定理
前: 幾何的定義による証明
2014-01-03