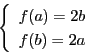![]() を整数とするとき,次のことを示せ.
を整数とするとき,次のことを示せ.
- (1)
-
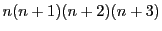 は24の倍数である.
は24の倍数である.
- (2)
 が奇数ならば,
が奇数ならば, 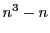 は24の倍数である.
は24の倍数である.
- (3)
 が2でも3でも割り切れないならば,
が2でも3でも割り切れないならば, 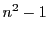 は24の倍数である.
は24の倍数である.
- (4)
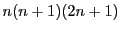 は6の倍数である.
は6の倍数である.
- (5)
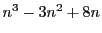 は6の倍数である.
は6の倍数である.
![]() を整数とするとき,次のことを示せ.
を整数とするとき,次のことを示せ.
![]() は互いに素な正の整数とするとき,次の問に答えよ.
は互いに素な正の整数とするとき,次の問に答えよ.
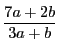 は既約分数である.
は既約分数である.
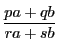 は既約分数である.
は既約分数である.
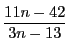 が既約分数にならないような
自然数
が既約分数にならないような
自然数
![]() を
を ![]() の素因数べきへの分解とする.
以下の命題を示せ.
の素因数べきへの分解とする.
以下の命題を示せ.
古代ギリシアの数学では整数 ![]() の約数(1を入れて
の約数(1を入れて![]() 自身を入れない)の和が
自身を入れない)の和が ![]() に等しいとき
に等しいとき
![]() を 完全数 と称していた.すなわち練習問題4 の記号では
を 完全数 と称していた.すなわち練習問題4 の記号では
次のことを示せ.
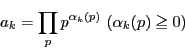
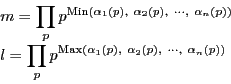
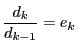 (ただし
(ただし
正の数
![]() に対して 数列
に対して 数列
![]() を次のように定義する.
を次のように定義する.
![]()
![]() について
について
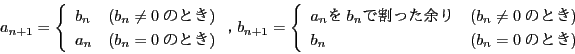
条件 ![]() を満たす正の整数
を満たす正の整数 ![]() から数列
から数列 ![]() を
を
![]()
また,数列 ![]() を
を
![]() に
よって定める.このとき,以下のことがらを示せ.
に
よって定める.このとき,以下のことがらを示せ.
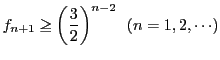
互いに異なる ![]() 個(
個(![]() )の正の数の集合
)の正の数の集合
![]() が次の性質をもつという.
が次の性質をもつという.
「このとき,から相異なる要素
をとれば
の少な くとも一方は必ず
に属する」
互いに異なる ![]() 個(
個(![]() )の実数の集合
)の実数の集合
![]() が次の性質をもつという.
が次の性質をもつという.
「このとき,から相異なる要素
,
をとれば
,
の少な くとも一方は必ず
に属する」
自然数を要素とする空集合でない集合![]() が次の条件(i),(ii)を満たしているとする.
が次の条件(i),(ii)を満たしているとする.
![]() を互いに素な正整数とする.
を互いに素な正整数とする.
![]() は互いに素な正の整数とする.
は互いに素な正の整数とする.
![]() は正の整数とし
は正の整数とし ![]() は互いに素であるとする.
は互いに素であるとする. ![]() は整数で,
は整数で, ![]() を満たすものとする.このとき次のことを証明せよ.
を満たすものとする.このとき次のことを証明せよ.
![]() は互いに素な整数とし,
は互いに素な整数とし, ![]() とする.座標平面内の集合
とする.座標平面内の集合 ![]() を
を
![]() 平面上の点で
平面上の点で ![]() 座標,
座標, ![]() 座標がともに整数である点を格子点という.
座標がともに整数である点を格子点という.
![]() は整数で
は整数で ![]() とし,直線
とし,直線
座標平面において,![]() 座標,
座標,![]() 座標がともに整数である点を格子点と呼ぶ.
座標がともに整数である点を格子点と呼ぶ.
四つの格子点
![]() を考える.ただし,
を考える.ただし,![]() は正の整数で,その最大公約数は1である.
は正の整数で,その最大公約数は1である.
![]() 平面上,
平面上, ![]() 座標,
座標, ![]() 座標がともに整数であるような点
座標がともに整数であるような点 ![]() を格子点と呼ぶ.
を格子点と呼ぶ.
各格子点を中心として半径 ![]() の円がえがかれており,
傾き
の円がえがかれており,
傾き
![]() の任意の直線はこれらの円のどれかと共有点をもつという.
このような性質をもつ実数
の任意の直線はこれらの円のどれかと共有点をもつという.
このような性質をもつ実数 ![]() の最小値を求めよ.
の最小値を求めよ.
自然数 ![]() を2の累乗と奇数の積として
を2の累乗と奇数の積として
![]() と表すとき,
と表すとき, ![]() と定める.
と定める.
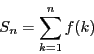
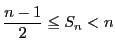 であることを示せ.
であることを示せ.
自然数 ![]() の約数の個数を
の約数の個数を ![]() とする.
とする. ![]() の約数をすべて並べて得られる 数列を
の約数をすべて並べて得られる 数列を
![]() とする.したがって,
とする.したがって,
![]() ,
, ![]() ,
,
![]() である.このとき,
である.このとき,
![]() に対する次の二つの条件(イ),(ロ)は互いに同値((イ)
に対する次の二つの条件(イ),(ロ)は互いに同値((イ) ![]() (ロ))であることを示せ.
(ロ))であることを示せ.
(イ) ![]() は60の倍数である.
は60の倍数である.
(ロ) ![]() は6個以上の約数を持ち,
は6個以上の約数を持ち,
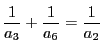 となる.
となる.
![]() はすべて自然数で,
はすべて自然数で,
自然数![]() について,等式
について,等式![]() が成り立ち,
かつ
が成り立ち,
かつ![]() は互いに素とする.このとき,次のことを証明せよ.
は互いに素とする.このとき,次のことを証明せよ.
正の整数 ![]() に対し,
に対し, ![]() の正の約数全体の和を
の正の約数全体の和を ![]() で表す.
ただし,1および
で表す.
ただし,1および ![]() 自身も約数とする.たとえば
自身も約数とする.たとえば ![]() であり,
であり,
![]() ならば15の正の約数は1,3,5,15なので
ならば15の正の約数は1,3,5,15なので![]() となる.次の問いに答えよ.
となる.次の問いに答えよ.