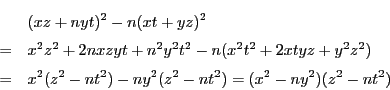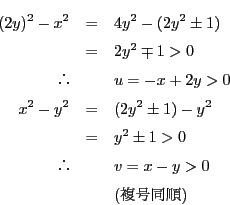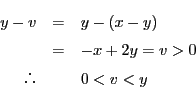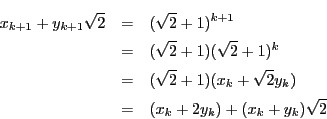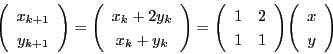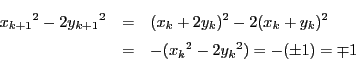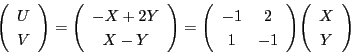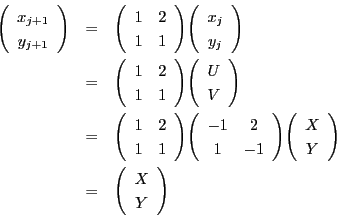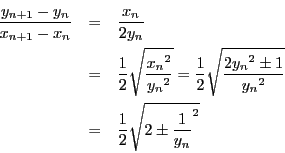次: 出典と文献
上: 解答
前: 演習問題解答
次: 出典と文献
上: 解答
前: 演習問題解答
解答 2 (問題
2)
- (1)
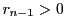 のとき,
のとき,
したがって,
となり, 各 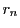 は自然数または0であるから, 高々
は自然数または0であるから, 高々 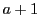 回
この操作を繰り返すとこれは0となる. つまり,
回
この操作を繰り返すとこれは0となる. つまり,
となる整数 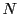 が存在する.
が存在する.
- (2)
 についての帰納法で示す.
についての帰納法で示す.
-
- (i)
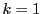 のとき,
のとき,
なので, 不等式は成り立つ. 次に, 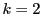 のとき,
のとき,
よって, 不等式は成り立つ.
- (ii)
-
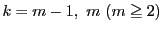 のときの不等式の成立, すなわち,
のときの不等式の成立, すなわち,
を仮定する. このとき,
となるので, 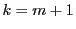 のときも成立する.
のときも成立する.
- (iii)
- よって, (i), (ii)より,
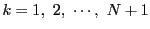 の
すべての
の
すべての  に対して不等式が成り立つ.
に対して不等式が成り立つ.
- (3)
 に関する帰納法で示す.
に関する帰納法で示す.
-
- (i)
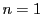 のとき,
のとき,
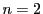 のとき,
のとき,
よって, いずれの場合も不等式は成り立つ.
- (ii)
-
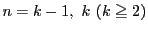 のときの不等式の成立, すなわち
のときの不等式の成立, すなわち
を仮定する. このとき
よって, 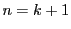 のときも不等式は成り立つ.
のときも不等式は成り立つ.
- (iii)
- よって, (i), (ii)より, すべての自然数
 に対して不等式が成り立つ.
に対して不等式が成り立つ.
- (4)
- (2)より,
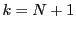 のとき,
のとき,
よって, (3)より,
で, 両辺の底を 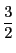 とする対数をとれば,
とする対数をとれば,
注意 9.2.1
この入試問題は,ユークリッドの互除法で割り算をどれくらい行えばよいかを評価するものである.
いちばん長くなるのが,割り算での商が常に 1 になるときで,あまりの列を逆にたどればいわゆる
フィボナッチ数列になるときである.このことを問う本格的な問題である.
解答 3
問題
3
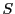
に属する最小の数を

とする.
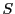
の任意の要素

をとり,

を

で割り商が

,余りが

とする.
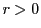
とする.
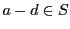
であり,自然数
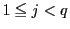
に対して
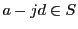
なら
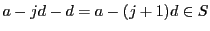
なので,数学的帰納法で
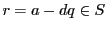
である.

が
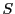
に属する正で最小の整数という仮定に反する.よって
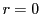
である.
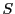
のすべての要素は

の倍数である.
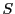 に属する最大の要素を
に属する最大の要素を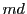 とおく,
とおく,
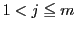 の整数に対して
の整数に対して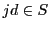 なら
なら
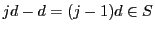 なので
なので
はすべて
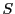
に属する.要素の個数を考え
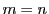
であり
となる.
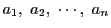
の順序を適当に変えれば
初項

,公差

の等差数列になる.
※ 大小の順で並べ替えて示してもよい.
解答 5
問題
5
自然数
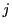
に対して
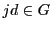
なら
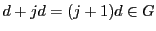
なので,数学的帰納法によって
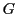 の任意の要素
の任意の要素 をとり,
をとり, を
を で割り商が
で割り商が ,余りが
,余りが とする.
とする.
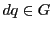
なので
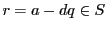
である.
ここで
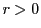
とすると

が
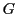
に属する正で最小の整数という仮定に反する.よって
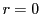
である.
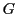
のすべての要素は

の倍数である.
が示され,題意が証明された.
解答 7 (問題
7)
- (1)
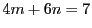 においてどのような整数
においてどのような整数 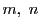 に対しても左辺は2で割り切れる.
一方右辺はつねに2で割ると1余る.ゆえにこの等式を満たす整数
に対しても左辺は2で割り切れる.
一方右辺はつねに2で割ると1余る.ゆえにこの等式を満たす整数 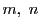 は存在しない.
は存在しない.
- (2)
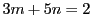 を満たすひと組の
を満たすひと組の 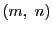 として
として 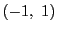 がとれる.
がとれる.
任意の解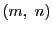 に対して
に対して
で辺々引くと,
3と5は互いに素なので, 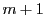 が5の倍数.これを
が5の倍数.これを 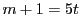 とおく.
とおく.
このとき 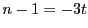 となる.つまり
となる.つまり
と表される.逆にこの形をしたものがもとの方程式を満たすことは明らか.
ゆえにすべての解は
- (3)
- 背理法で示す.
ゆえに対偶が示されたので,
である.
- (4)
- 二つの集合
この  に対して
に対して 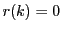 なら
なら 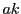 が
が  の倍数.
の倍数.
 と
と  は互いに素なので
は互いに素なので  が
が  の倍数となるが,
の倍数となるが,
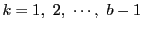 よりあり得ない.
したがって
よりあり得ない.
したがって 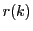 は
は  で割った余りでしかも0でないので
で割った余りでしかも0でないので
一方(3)より
なので,
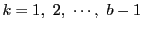 に対して
に対して 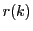 はすべて異なる.
つまり集合
はすべて異なる.
つまり集合 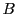 の個数は
の個数は 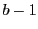 で,集合
で,集合  の個数と等しい.
の個数と等しい.
したがって 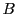 の元のなかに
の元のなかに
となるものがある.このとき
つまり
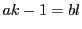 となる
となる 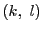 が存在した.
が存在した.
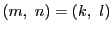 という解が存在した.
という解が存在した.
解答 9 (問題
9)
- (1)
-
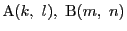 とする.
とする.
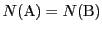 より
より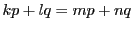 である.つまり
である.つまり
であるが,  と
と  が互いに素なので
が互いに素なので 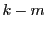 が
が  の倍数でなければならない.
ところが
の倍数でなければならない.
ところが
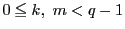 なので
なので
である.この範囲で  の倍数は0しかない.つまり
の倍数は0しかない.つまり 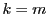 .
.
その結果 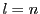 となり,
となり,
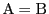 であることが示された.
であることが示された.
- (2)
-
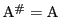 とする.つまり
とする.つまり
これから
となり,  と
と  は公約数2をもち互いに素であることに反する.ゆえに
は公約数2をもち互いに素であることに反する.ゆえに
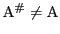 である.
である.
- (3)
- 条件
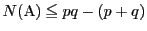 は
は
である.他方,条件
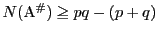 は
は
である.ここで
ゆえに2つの条件が同値であることが示され,題意が示された.
- (4)
- (3)から
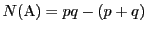 なら
なら
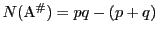 となる.つまり等号が成立すると
となる.つまり等号が成立すると
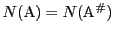 である.
(1)から
である.
(1)から
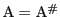 となるが,これは(2)の結果と矛盾する.
ゆえに
となるが,これは(2)の結果と矛盾する.
ゆえに
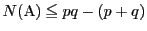 で等号は成立しない.
で等号は成立しない.
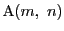 のとき
のとき
なので,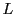 の元
の元 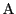 と
と
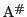 は1:1に対応する.(4)から
は1:1に対応する.(4)から
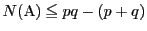 となる
となる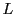 の元
の元 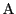 の個数は
の個数は 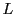 の半分である.
の半分である.
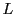 は明らかに
は明らかに 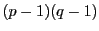 個からなるので,求める元の個数は
個からなるので,求める元の個数は
注意
条件
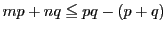 は書きかえると は書きかえると
である.
(4)の解答中にあるように,直線
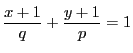 上には格子点がないので,この直線が 上には格子点がないので,この直線が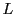 の格子点を二分することがわかる. の格子点を二分することがわかる.
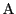 と と
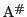 の対応は,
この二分された二つの領域の中の格子点の一対一対応である. の対応は,
この二分された二つの領域の中の格子点の一対一対応である.
|
解答 10 (問題
10)

をひとつ固定する.
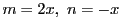
は
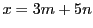
を満たす.
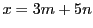 を満たす任意の解を
を満たす任意の解を 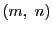 とする.
とする.
この辺々を引いて,
3 と 5 は互いに素なので,ある整数

によってつぎのようにおけなければならない.
つまり

を表す
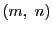
は整数

によって次のように表される.
この
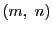
が

を表すことも明らかである.
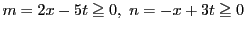 なので
なので
したがってこの範囲に整数

が存在することと,

が非負整数
を用いて表わせることが同値である.
つまり
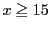
なら必ず条件を満たす整数

がとれる.したがって
について調べればよい.
したがって表せないものはつぎの四つである.

を3で割った余りで分類して考える.
したがってのこるのは1,2,4,7 である.ところが
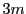
のとりうる値は0,3,6,9,…
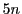
のとりうる値は0,5,10,15,…
であるから,明らかに1,2,4,7は
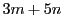
の形で表せない.
解答 11 (問題
11)
- (1)
-
であるから,格子点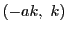 は
は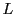 上にある.
上にある.
- (2)
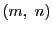 を
を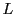 上の任意の格子点とする.つまり
上の任意の格子点とする.つまり
である.
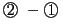 をとる.
をとる.
 の約数は
の約数は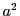 の約数であり,
の約数であり,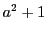 の約数ではありえないので
の約数ではありえないので
 と
と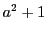 は互いに素である.
は互いに素である.
したがって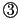 より
より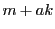 は
は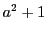 の倍数である.
整数
の倍数である.
整数 を用いて
を用いて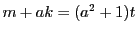 とおける.このとき
とおける.このとき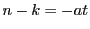 となる.
となる.
つまり 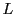 上の格子点は整数
上の格子点は整数  によって,
によって,
と表される.逆にこのように表されるものが 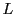 上にあることは明らかである.
上にあることは明らかである.
題意をみたす格子点が存在するのは,
をみたす  が存在することと同値である.つまり
が存在することと同値である.つまり
ここで 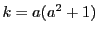 のとき
のとき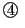 は
は
となる.よって条件をみたす整数  が存在せず,
題意をみたす
が存在せず,
題意をみたす 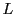 上の格子点も存在しない.
上の格子点も存在しない.
- (3)
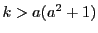 のとき
のとき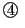 の左辺から右辺を引くと,
の左辺から右辺を引くと,
したがって条件をみたす  がつねに存在し,
題意をみたす
がつねに存在し,
題意をみたす 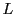 上の格子点も存在する.
上の格子点も存在する.
解答 12 (問題
12)
- (1)
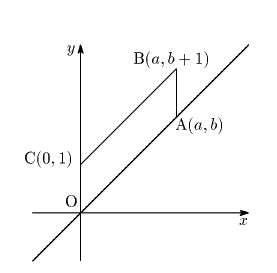

と

が互いに素であるから,
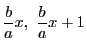
が整数となるのは

が

の倍数であるときにかぎる.直線OA,CBの方程式が
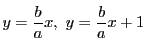
なので,
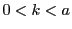
の範囲の整数

に対し,直線
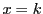
と直線 OA, CBの交点はいずれも格子点ではない.したがって, 直線
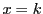
のOABCの内部にある部分には,ちょうど一つの格子点がある.よって
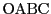
の内部には
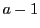
個の格子点がある.
- (2)
- OABCの内部の格子点を
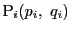 とおく.
とおく.
である.
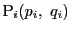 は領域
は領域 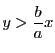 にあるので,
にあるので,
よって,
である.ここで等号が成立する 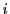 が存在することを示す.
が存在することを示す.
まず,
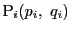 に対し,
に対し,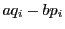 がすべて異なることを示す.
がすべて異なることを示す.
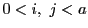 に対して
に対して 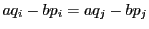 ならば,
ならば,
となる. と
と  が互いに素であるから,
が互いに素であるから,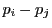 は
は  の倍数である.
ところが,
の倍数である.
ところが,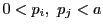 より,
より,
であるから, の倍数は
の倍数は 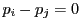 以外にないことがわかる.
よって,
以外にないことがわかる.
よって,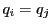 も成り立ち,
も成り立ち,
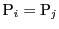 がわかる.
したがって,集合
がわかる.
したがって,集合 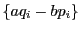 の元の個数は
の元の個数は 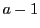 である.
である.
一方,
なので,集合 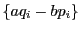 は集合
は集合 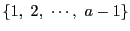 に含まれ,
かつ元の個数が一致する.よって二つの集合は一致し,かならず
に含まれ,
かつ元の個数が一致する.よって二つの集合は一致し,かならず 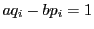 となる番号
となる番号 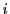 がある.
したがって,求める最小値は,
がある.
したがって,求める最小値は,
参考
・等号成立の別証
とする.
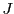
の元で正で最小のものを
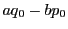
とする.
任意の 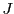 の元
の元 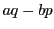 を
を 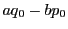 で割る.
で割る.
ここで,
であるから,
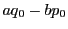
の最小性によって,
である.つまり
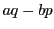
は,
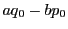
の倍数である.
ところが
同じく

も
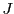
の元であるから,
となり,

と

が互いに素であるから,
この
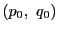
に対して整数

を用いて,
とおくと,
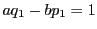
であり,

を適当にとると
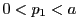
にできる.
このとき
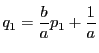
より,
となるので,
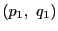
は, OABCの内部にある.
解答 13 (問題
13)
傾きが
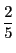
である直線
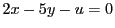
を
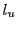
と表すことにする.
このとき, 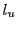 と格子点
と格子点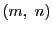 との距離は,次の式で与えられる.
との距離は,次の式で与えられる.
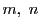
が変化するとき,
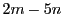
は任意の整数値をとりうる.実際,任意の整数

に対して
が成り立つ.
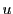
を整数部分と小数部分に分けて
と書くことにする.したがって上に述べたことから
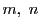
が変化するとき,
ゆえに1は
そしてこの等号が成立する
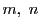
が必ず存在する.したがって
に円の半径をとれば,直線
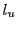
は円のいずれかと共有点をもつ.
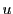 の値に関わらず共有点をもつためには
の値に関わらず共有点をもつためには 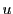 を動かしたときの
を動かしたときの
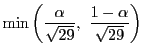 の
最大値以上に
の
最大値以上に  をとればよい.
をとればよい.
明らかに
で等号は
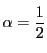
のときである.
したがって
であれば,
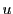
に関わらず直線
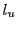
は円のいずれかと共有点をもつ.求める

の最小値は
注意 9.2.2
論証の根幹に,
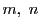
が変化するとき,
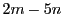
は任意の整数値をとりうる,事実がある.
解答 14 (問題
14)
- (1)
- 集合
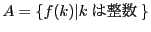 とおく.明らかに
とおく.明らかに 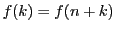 である.
である.
さらに
したがって
であるから
次に
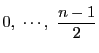 で
で 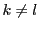 のとき
のとき
となるのは
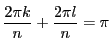 のときのみ.
のときのみ.
このとき
となり,  が奇数であることに反する.
ゆえに
が奇数であることに反する.
ゆえに
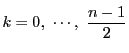 に対して
に対して 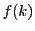 はすべて異なる.
はすべて異なる.
- (2)
- 集合
とおく.定義から
である.
ここで
したがって集合  の考察と逆に考えて
の考察と逆に考えて
である.
を示す.
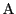 の任意の元
の任意の元 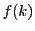 に対して
に対して 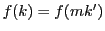 となる
となる
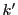 が存在すればよい.
が存在すればよい.
となる 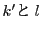 が存在すれば十分である(十分条件で成り立つ).
これは
が存在すれば十分である(十分条件で成り立つ).
これは
となる 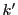 と
と 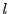 が存在することである.
が存在することである.
 と
と  は互いに素なので
は互いに素なので 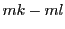 が
が  の倍数になれば
の倍数になれば
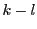 自身が
自身が  の倍数でなければならないので
の倍数でなければならないので
を  で割った余りはすべて異なる.ゆえに必ず余りが
で割った余りはすべて異なる.ゆえに必ず余りが  になるものが存在する.
になるものが存在する.
となり
である.つまり集合として  と
と 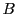 は等しく
は等しく  によらず一定である.
によらず一定である.
注意 9.2.3
ここは演習問題7とは違うやり方で
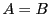
を示した.
いずれも一次不定方程式の解の存在が基本的事実である.
解答 16 (問題
16)
- (1)
-
ゆえに
- (2)
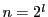 とする.(1)と同様に
とする.(1)と同様に
- (3)
-
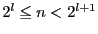 とする.
とする.
次に
以上から
解答 17 (問題
17)
- (1)
- (イ)⇒(ロ)を示す.
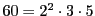 であるから
であるから  が60の倍数なら
が60の倍数なら
である.
- (2)
- (ロ)⇒(イ)を示す.
条件式から
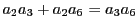 である.これを変形すると,
である.これを変形すると,
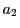 は必ず素数だから,
は必ず素数だから, 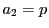 とおくと,
とおくと, 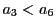 より
より
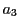 としてあり得るのは
としてあり得るのは
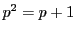 は整数解がない.よって
は整数解がない.よって  と異なる素数.
と異なる素数.
 と
と 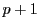 がともに素数になるのは
がともに素数になるのは 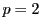 のみ.このとき,
のみ.このとき,
なので, 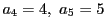 以外にない.
よって
以外にない.
よって  は少なくとも
は少なくとも 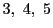 を因数にもつ.つまり60の倍数である.
を因数にもつ.つまり60の倍数である.
解答 19 (問題
19)
- (1)
-
左辺は  の倍数.
の倍数.  と
と  が互いに素なので
が互いに素なので 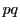 は
は  の倍数である.
の倍数である.
- (2)
 と
と  の最大公約数を
の最大公約数を 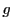 とし,
とし,
とおく.このとき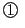 は
は
となる.つまり
(1)と同様に 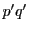 が
が  の倍数になる.
の倍数になる.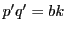 とおく.このとき
とおく.このとき 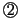 から
から
ここで 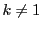 なら
なら
ゆえに 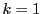 となり,
となり, 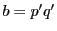 ,
,
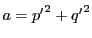 .つまり
.つまり
これは自然数である.
解答 21 (問題
21)
- (1)
 の約数を
の約数を
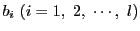 とする.
2と
とする.
2と は互いに素なので
は互いに素なので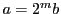 の約数のすべては,
の約数のすべては,
で与えられる.
- (2)
 が2以上の整数なので
が2以上の整数なので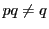 である.したがって
である.したがって  と
と 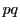 は
は
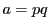 の異なる約数である.
の異なる約数である.
等号が成り立つのは,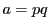 の約数が
の約数が  と
と  のみのときである.
1とその数自身は必ず約数になるので
のみのときである.
1とその数自身は必ず約数になるので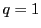 で,
かつ1とその数自身以外の約数がないので
で,
かつ1とその数自身以外の約数がないので は素数でなければならない.
は素数でなければならない.
- (3)
- (1)から
ここで,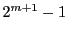 と
と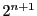 は互いに素なので,
は互いに素なので,  は
は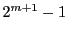 を約数にもつ.
を約数にもつ.
 についも同様.
についも同様.
とおける.このとき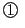 から
から
一方(2)から
である.
より 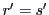 で3が等号になる.
で3が等号になる.
(2)より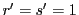 なので2から
なので2から
解答 24 (問題
24)
- (1)
-
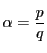 とする.ここで
とする.ここで 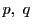 は互いに素とする.
は互いに素とする.
右辺は  の倍数で
の倍数で  は
は  と互いに素なので
と互いに素なので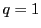 .
.
つまり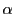 は整数である.
は整数である.
- (2)
- 背理法でしめす.
方程式 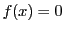 が有理数の解をもてば(1)からそれは整数である.
が有理数の解をもてば(1)からそれは整数である.
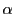 を
を  で割って
で割って
とおく. 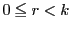 である.
である.
ゆえに 個の整数
個の整数
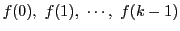 のどれかが
のどれかが  で割り切れる.
で割り切れる.
さらに
であるから
 個の整数
個の整数
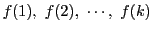 のどれかが
のどれかが
 で割り切れなければならない.
で割り切れなければならない.
これは条件と矛盾するので,題意が示された.
解答 25 (問題
25)
解1
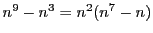 なので
なので  が3の倍数なら明らかに9の倍数である.
が3の倍数なら明らかに9の倍数である.
3の倍数でないときに示す.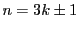 とおく.
とおく.
ゆえに
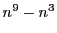
は9で割り切れる.
解2

が3の倍数なら
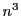
が9の倍数,

が3で割って1余る数なら
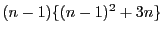
が9の倍数,

が3で割って2余る数なら
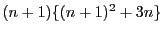
が9の倍数となり,
つねに3の倍数である.
解答 26 (問題
26)
-
-
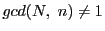 となるものは,
となるものは, または
または の倍数である.
したがって
の倍数である.
したがって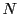 より小さい自然数
より小さい自然数 では
では
である.
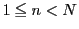 の範囲で
の範囲で
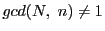 となるものが(i)より
となるものが(i)より
ある.同じ範囲で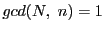 となるものはそれらを除いたものである.
となるものはそれらを除いたものである.
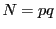 なので(ii)から
なので(ii)から
つまり,
よって,
 と
と を解としてもつ二次方程式は未知数を
を解としてもつ二次方程式は未知数を とすれば次のようになる.
とすれば次のようになる.
-
である.よって
解答 27 (問題
27)
- (1)
-
である.ゆえに6個.
- (2)
 が6と互いに素なら
が6と互いに素なら
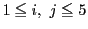 に対して
に対して
である.ゆえに
となる.
一方
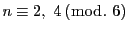 のときは
のときは 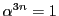 ,
,
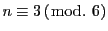 のときは
のときは 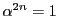 である.
である.
解答 28 (問題
28)
- (1)
- 条件(イ)より
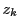 は1と異なる1の
は1と異なる1の  乗根である.
乗根である.
とおくと, 1と異なる1の  乗根は
乗根は
一意に表される.
このとき条件(ロ)は
となる.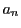 は
は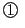 の解
の解
の個数を表す.
であるから,
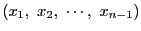 を
を
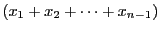 が
が
 の倍数でないようにさえ選べば,一組の解が得られる.
の倍数でないようにさえ選べば,一組の解が得られる.
ここで 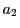 を求める.
を求める. 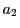 は
は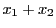 がpの倍数となる
がpの倍数となる
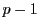 個である.
個である.
- (2)
- (1)から
- (3)
-
を解く. 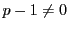 なので
なので
これから
[漸化式の別解]
の解を二つに分類する.
-
- (i)
-
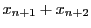 がpの倍数のとき.この
がpの倍数のとき.この
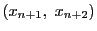 は
は 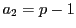 個あり,その各に対し結局
個あり,その各に対し結局
となる.この場合の個数は
- (ii)
-
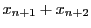 がpの倍数でないとき.
がpの倍数でないとき.
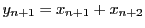 とおくと
とおくと
の解は 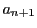 個あり.各
個あり.各 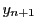 に対して
に対して
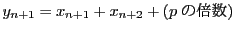 となる
となる
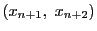 は
は 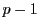 組ある.
組ある.
なぜなら 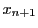 は
は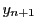 と同じにはとれない(同じにとると
と同じにはとれない(同じにとると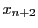 がとれない)が,逆に異なれば
がとれない)が,逆に異なれば
 と
と  で割ったの余りが等しい
で割ったの余りが等しい が一つ定まる.
が一つ定まる.
この場合の個数は
解答 31 (問題
31)
- (1)
- 自然数
 を7で割った商をそれぞれ
を7で割った商をそれぞれ  , 余りをそれぞれ
, 余りをそれぞれ 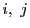 とおくと,
とおくと,
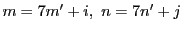 と書けて
と書けて
より, 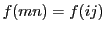 を得る. そこで, これを用いて, 自然数
を得る. そこで, これを用いて, 自然数  を7で割った余りで分類し,
を7で割った余りで分類し,
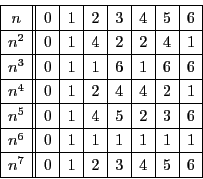
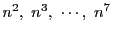 を7で割った余りを順に求めていくと, 下表のようになる.
を7で割った余りを順に求めていくと, 下表のようになる.
よって, すべての自然数  に対して
に対して
注意 9.2.4
これは言うまでもなく「フェルマの小定理」そのものである.文系入試問題であるので,実際に7で割った余りの表を作ることで論証した.
他の演習問題にあるように,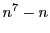 が7の倍数になることを
が7の倍数になることを に関する数学的帰納法で示すことができる.
に関する数学的帰納法で示すことができる.
- (2)
- (1)の結果より, すべての自然数
 に対して,
に対して, 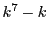 は7の倍数であるから
は7の倍数であるから
よって, 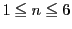 の範囲で考えれば十分である. ここで, (1)の表を利用すると
の範囲で考えれば十分である. ここで, (1)の表を利用すると
となるから, 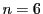 をとれば
をとれば
注意 9.2.5
本問の(2)は正整数

が3個の平方数の和とならないための十分条件を与えている.
しかし(1)の28が示すように,これは必要条件ではない.
では正整数 が3個の平方数の和とならないための必要十分条件は何か.
実はそれもガウスが解決している.
が3個の平方数の和とならないための必要十分条件は何か.
実はそれもガウスが解決している.
これが
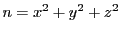
となる正整数
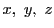
が存在しないための必要十分条件である.
『数論講義』(J.P,Serre)に載っている.
解答 35 (問題
35)
解1
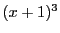
を
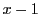
で割って
これから
となる.
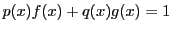
と辺々引いて
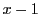
と
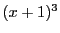
は互いに素なので,ある整式
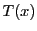
を用いて
と表され,またこの形のものは与式を満たす.ゆえに任意の解は
と表される.
次数最小のものは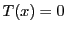 のときである.
のときである.
である.最高次数の係数が1で次数最小のものは
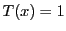
のときだから
である.
解2
与式に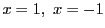 を代入して
を代入して
これから
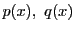
は,ある整式
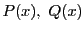
を用いて
と表される.これを与式に代入して
これから
次数を小さくとるために,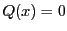 とおく.
とおく.
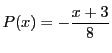 .
.
このとき
逆にこれは与式を満たす.
次に与式を満たす任意の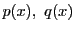 と,先に求めた一組の解を与式に代入し
と,先に求めた一組の解を与式に代入し
の辺々を引く(以下は同じ).
解答 36
問題
36
解1 (整式の除法を用いる方法)
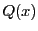 は2次式なので,
整式
は2次式なので,
整式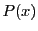 を
を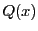 で割った余りは1次以下の整式である.
商を
で割った余りは1次以下の整式である.
商を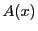 ,余りを
,余りを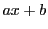 とする.
とする.
このとき
ところが
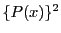
は
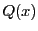
で割り切れるので
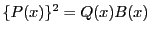
とおける.
これから
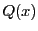
は2次式で,右辺は2次以下であるから,
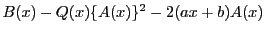
は定数である.これを
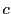
とする.
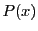 は
は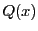 で割り切れないので右辺は定数0ではない.
つまり
で割り切れないので右辺は定数0ではない.
つまり である.よって
である.よって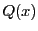 は
は
と表される.
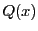
は2次式だから
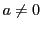
である.
このとき方程式
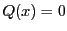
は重解

を持つ.
解2 (整式の整数論を用いる方法)
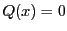 の解を
の解を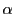 と
と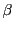 とし,
とし,
とおく.
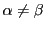
と仮定する.
このとき
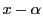
と
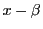
は互いに素である.
よって任意の整式
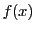
について
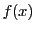
が
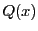
で割りきれることと,
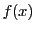
が
で割り切れかつ
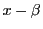
で割り切れることが同値である.
もし
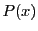
が因数
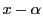
をもたなければ,整式における素因数分解の一意性によって,
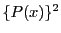
も因数
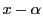
をもたない.
よってもし
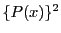
が因数
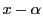
をもてば,
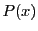
が因数
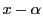
をもつ.
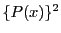 は
は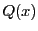 で割り切れるので,
で割り切れるので,
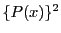 が因数
が因数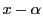 と
と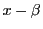 をもち,
その結果
をもち,
その結果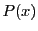 が因数
が因数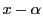 と
と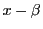 をもつ.
をもつ.
ところがこれは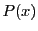 が
が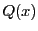 で割りきれることを意味し,仮定と矛盾する.
よって
で割りきれることを意味し,仮定と矛盾する.
よって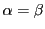 であり,2次方程式
であり,2次方程式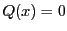 は
は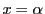 を重解にもつ.
を重解にもつ.
解答 37
問題
37
解1 (整式の除法を用いる方法)
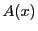 と
と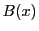 を
を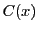 で割った商と余りをそれぞれ
で割った商と余りをそれぞれ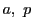 と
と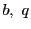 とし,
とし,
とおく.
それぞれ1次式であるので,
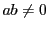
である.
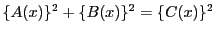
より
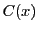
を
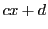
とすると,

で,両辺の
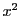
の係数の比較より
これから
である.
このとき
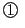
は
となる.両辺の

の係数比較から
その結果,
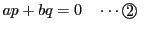
となり,さらに
である.ここで
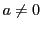
なので
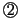
から
これを
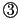
に代入して
よって
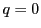
となり,
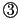
から
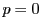
.
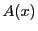 と
と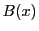 はともに
はともに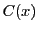 の定数倍であることが示された.
の定数倍であることが示された.
解2 (整式の整数論を用いる方法)
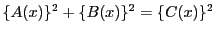 より
より
である.
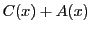
も
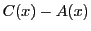
も1次以下の整式であるから
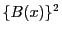
の定数倍になることはない.
したがって定数
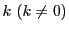
が存在して
と表される.
これから
である.
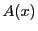
も
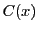
も1次式なので
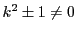
である.
となり,
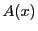
と
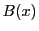
はともに
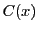
の定数倍であることが示された.
解答 38
問題
38
解1
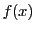 を
を 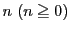 次,
次,
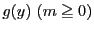 を
を  次とし
次とし
とおく.
条件は
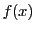
と
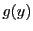
で対称なので
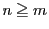
とする.
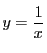 のとき条件は
のとき条件は
となる.
のなかでこの順に見て最初に0でない係数を
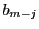
とする.上の条件は
これから
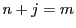
であるが
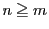
より
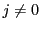
なら
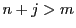
で不可.
つまり
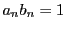
.整数係数なので
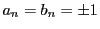
で
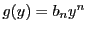
.
このとき 1より
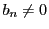
なので
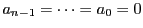
.
ゆえに
解2
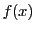 を
を 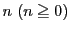 次,
次,
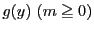 を
を  次とし
次とし
とおく.
条件は
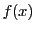
と
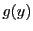
で対称なので
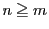
とする.
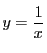 のとき条件は
のとき条件は
となる.
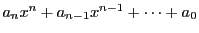 も
も
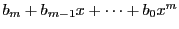 も
も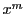 の約数となるが,
の約数となるが, は既約なので,ともに
は既約なので,ともに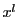 の定数倍という形をしている.
次数を考えると
の定数倍という形をしている.
次数を考えると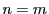 で
で
である.さらに
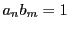
となり係数が整数なのでともに
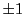
である.ゆえに
解答 39 (問題
39)
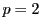
のとき.
で,
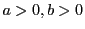
よりこれは実数とはなり得ない.
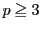 とする.二項定理より
とする.二項定理より
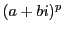 が実数とすると
が実数とすると
である.ところが
ただし 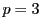 のとき中央の項は0とする.
のとき中央の項は0とする.
一般に
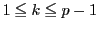 に対して
に対して
であるが,

が素数なので
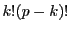
は

と互いに素である.しかも右辺は整数なので
が整数.つまり
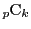
は

の倍数である.
したがってある整数
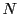
が存在して
となる.これからまず

が

の倍数である.そこで
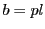
とおく.
つまり
となる.これから

も

の倍数である.
 も
も  も
も  の倍数となり,
の倍数となり,  ,
,  が互いに素であることと矛盾した.
が互いに素であることと矛盾した.
以上から 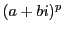 は実数ではあり得ないことが示された.
は実数ではあり得ないことが示された.
解答 41 (問題
41)
- (1)
-
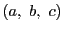 は等式(Q)を満たすので
は等式(Q)を満たすので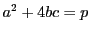 である.ゆえに
である.ゆえに
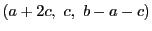 もまた等式(Q)を満たす.
もまた等式(Q)を満たす.
- (2)
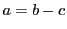 とする.
とする.
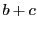 が自然数なので,
が自然数なので,  が素数であることに反する.
が素数であることに反する.
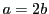 とする.
とする.
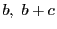 が自然数なので,
が自然数なので,  が素数であることに反する.
が素数であることに反する.
ゆえに,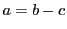 や
や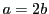 を満たすことはない.
を満たすことはない.
- (3)
- 手続きのうち,(i)と(iii)は,必ず変化する.変化しないときは手続き(ii)で
となるときにかぎる.これから 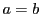 .このとき
.このとき
 は素数,かつ
は素数,かつ 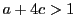 なので
なので 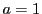 .
このとき
.
このとき
から 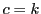
したがって題意をみたすものは
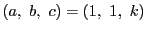 であり,
これ以外には存在しない.
であり,
これ以外には存在しない.
- (4)
- 等式(Q)を満たす自然数の組
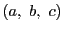 に対して上の手続きを1回行ったものを
に対して上の手続きを1回行ったものを
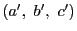 ,2回行ったものを
,2回行ったものを
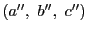 と記す.
これらは等式(Q)を満たす.
と記す.
これらは等式(Q)を満たす.
-
- (i)
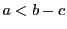 ならば
ならば
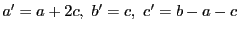 .このときは
.このときは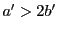 なので
なので
- (ii)
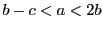 ならば
ならば
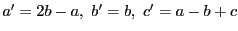 .このときは
.このときは
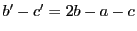 なので
なので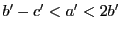 となる.ゆえに
となる.ゆえに
- (iii)
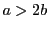 ならば
ならば
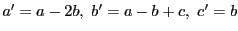 .このときは
.このときは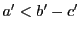 なので
なので
したがって2回の操作で元の組に戻る.
したがって組の各元はたがいにこの操作で入れ替わるものの組に分けることができる.
この操作で変わらないものはただ一つなので,その他は2つずつの組になる.
したがって等式(Q)を満たす自然数3つの組の全体の個数は奇数である.
- (5)
- 等式(Q)は
 と
と 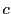 に関して対称である.したがって組
に関して対称である.したがって組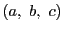 が等式(Q)を満たせば,組
が等式(Q)を満たせば,組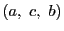 も満たす.
も満たす.
(3)から等式(Q)を満たす自然数3つの組は少なくとも一組は存在し,
(4)からそのような組の全体の個数は奇数である.
もしすべての組が 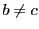 なら,2つずつが組になって
そのような組の全体の個数は偶数になる.
なら,2つずつが組になって
そのような組の全体の個数は偶数になる.
したがって,そのような組のなかには
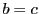 となるものが存在する.このとき
となるものが存在する.このとき
と表される.
注意 9.2.6
この問題は定理47 の別証明になっている.
出典:
D. Zagier,
A one-sentence proof that every prime
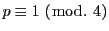 is a sum of two squares,
is a sum of two squares,
Amer. Math. Monthly 97 (1990) 144.
またこれは次の書でも紹介されている.
『数論の3つの真珠』(ヒンチン著、蟹江訳、日本評論社)p.128
解答 42 (問題
42)
- (1)
-
- (i)
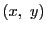 を任意の整数解とする.
を任意の整数解とする.
で
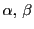 が互いに素な正の整数であるから,
が互いに素な正の整数であるから,
 は
は 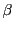 の倍数である.
の倍数である. 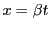 とおく.このとき
とおく.このとき 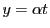 となる.
逆にこの形をしている
となる.
逆にこの形をしている 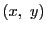 は方程式を満たす.
は方程式を満たす.
- (ii)
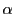 を
を 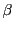 で割り商が
で割り商が  余りが
余りが 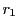 とすると
とすると
一方
正の有理数の整数部分と小数部分は一意だから
次に
なので,同様に 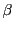 を
を 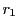 で割った商が
で割った商が 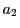 で,
余りを
で,
余りを 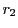 とすると
とすると
再び同様に考えると
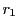 を
を 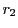 で割った商が
で割った商が 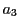 で,その余りを
で,その余りを 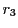 とすると
とすると
つまり
ゆえに
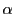 と
と 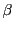 は互いに素なので
は互いに素なので 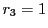
注意 9.2.7
ユークリッドの互除法の原理から
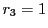
であるが,ここは直接確認した.
したがって
という除法の系列ができる.
このとき
つまり
- (2)
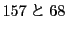 は互いに素である.
は互いに素である.
つまり
(1)より
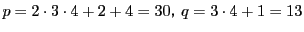 とおくと
とおくと
したがって
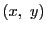 を
を 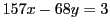 の任意の整数解とする.
の任意の整数解とする.
ゆえに(1)より
と書ける.
解答 43 (問題
43)
-
もし
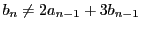 なら
なら
となる.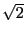 は無理数で右辺は有理数となり.矛盾.
は無理数で右辺は有理数となり.矛盾.
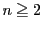 のとき
のとき
- (2)から
である.つまり
ここで(1)から
なので,これを用いて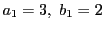 から
から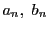 を順次求めると,
を順次求めると,
である.したがって
求める有理数は
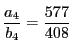
解答 44 (問題
44)
- 条件から
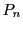 と
と 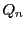 の最大公約数を
の最大公約数を  とし
とし
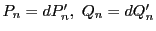 とする.
とする.
つまり 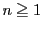 のとき,
のとき, 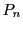 と
と 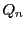 の最大公約数は
の最大公約数は 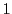 である.
である.
-
-
ここで 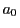 無理数なので,帰納的に定められた
無理数なので,帰納的に定められた
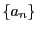 はすべて正の無理数である. また
はすべて正の無理数である. また
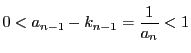 から
から 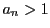 .
.
定め方から
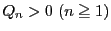 なので
なので
解答 45 (問題
45)
- (1)
- 四つの頂点を
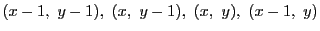 とする.
とする.
 を超えない最大の整数を
を超えない最大の整数を  とする.
とする. 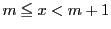 であるから
であるから
つまり区間 ![$[x-1,\ x]$](images/img4135.gif) には整数
には整数  が存在する.
が存在する.
 方向についても同様に
方向についても同様に ![$[y-1,\ y]$](images/img4136.gif) には整数
には整数  が存在する.
が存在する.
したがって,正方形(周をこめる)には少なくとも一つの
格子点 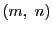 が存在した.
が存在した.
- (2)
- 辺の長さが
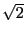 の正方形には半径
の正方形には半径
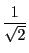 の円が
内接している.
の円が
内接している.
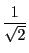 の円には,1辺の長さが1の正方形が内接する.
の円には,1辺の長さが1の正方形が内接する.
したがって(1)から少なくとも一つの格子点を含むことが示された.
解答 48 (問題
48)
-
- (1)
- 3頂点を
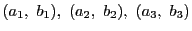 とする.
このとき面積
とする.
このとき面積 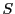 は
は
である.ゆえに 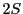 は整数である.
は整数である.
- (1)
- 3頂点の座標がすべて整数の組であるような正三角形が存在するとし,
その正三角形の面積を
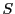 とする.(1)から
とする.(1)から 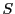 は有理数である.
は有理数である.
一方正三角形の1辺を  をすると
をすると
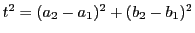 なので面積
なので面積 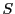 は
は
これは無理数である.
したがって(1)の結果と矛盾した.
ゆえに3頂点の座標がすべて整数の組であるような正三角形は存在しない.
- (3)
- 平面上で,5頂点の座標がすべて整数の組であるような正五角形は存在するとし,
正五角形の中心を原点に平行移動する.
隣りあう二つの頂点を
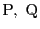 とする.
とする.
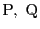 は
格子点であるから(1)と同様に
は
格子点であるから(1)と同様に
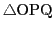 の面積は有理数である.
の面積は有理数である.
一方
ここで
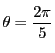 とすると,
とすると,
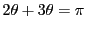 なので
なので
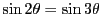 .つまり
.つまり
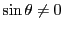 なので
なので
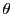 は鋭角なので
は鋭角なので
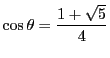 .ゆえに
.ゆえに
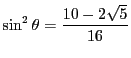 .これは無理数であり,したがって
.これは無理数であり,したがって
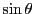 も無理数である.
も無理数である.
(2)と同様の矛盾が生じた.
よって,平面上で5頂点の座標がすべて整数の組であるような正五角形は存在しない.
解答 49 (問題
49)
- (1)
-
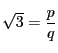 となる整数
となる整数  が存在したとして矛盾を示す.
以下特に断らなければ文字は整数を表す.
が存在したとして矛盾を示す.
以下特に断らなければ文字は整数を表す.
証明法1
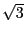 が無理数でない,つまり有理数とする.
が無理数でない,つまり有理数とする.
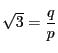 とおく.ここで
とおく.ここで と
と は互いに素であるとできる.
は互いに素であるとできる.
数 が3の倍数でなければ
が3の倍数でなければ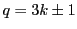 とおける.
とおける.
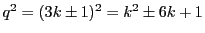 より3の倍数でない数
より3の倍数でない数 の平方
の平方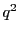 は3の倍数でない.
ところが左辺が3の倍数なので
は3の倍数でない.
ところが左辺が3の倍数なので  は3の倍数でなければならない.
は3の倍数でなければならない.
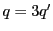 とおける.すると
とおける.すると
これから  も3の倍数となり,
も3の倍数となり,  と
と  が互いに素であることと矛盾した.
が互いに素であることと矛盾した.
ゆえに 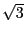 は無理数である.
は無理数である.
証明法2
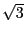 が無理数でない,つまり有理数とする.
が無理数でない,つまり有理数とする.
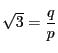 とおく(既約である必要はない).
とおく(既約である必要はない).
左辺の因数分解における因数3の個数は奇数である.
右辺の因数分解における因数3の個数は偶数である
これは矛盾である.ゆえに 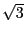 は無理数である.
は無理数である.
証明法3
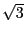 が無理数でない,つまり有理数とする.
が無理数でない,つまり有理数とする.
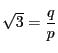 とおく(既約である必要はない)..
とおく(既約である必要はない)..
証明法1と同様に3の倍数でない数の平方は3の倍数でない.
ところが左辺が3の倍数なので  は3の倍数でなければならない.
は3の倍数でなければならない.
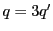 とおける.すると
とおける.すると
これから  も3の倍数となり
も3の倍数となり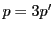 とおける.
とおける.
再び
となる.同様にして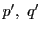 とも3の倍数である.これは何回でも繰り返される.
とも3の倍数である.これは何回でも繰り返される.
つまり  も
も  も3で無限回割れる.これは
も3で無限回割れる.これは 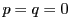 以外では不可能である.
以外では不可能である.
ゆえに 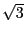 は無理数である.
は無理数である.
- (2)
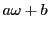 が有理数
が有理数 であるとする.
であるとする.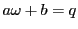 において
において
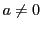 なので
なので
有理数の和,差,積,商は再び有理数なので,これは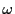 が無理数であることに矛盾した.
が無理数であることに矛盾した.
よって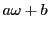 は無理数である.
は無理数である.
- (3)
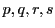 がすべて有理数と仮定する.
がすべて有理数と仮定する.
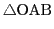 の面積を二通りの方法で求める.
の面積を二通りの方法で求める.
一方
である.ゆえに
が成り立たねばならない.つまり
である.ここで(2)から左辺は無理数である.一方,右辺0は有理数で矛盾である.
よって 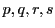 のうち少なくとも1つは有理数とならないことが示された.
のうち少なくとも1つは有理数とならないことが示された.
解答 (追加問題)



 次: 出典と文献
上: 解答
前: 演習問題解答
Aozora Gakuen
次: 出典と文献
上: 解答
前: 演習問題解答
Aozora Gakuen
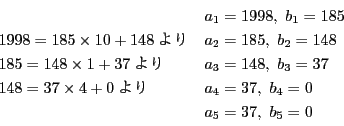
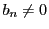 のとき
のとき 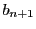 は
は 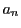 を
を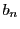 で割った余りであるから
余りの定義より,
で割った余りであるから
余りの定義より,
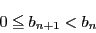
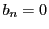 のとき 数列
のとき 数列 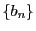 の定義から
の定義から 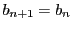 .
よって 任意の
.
よって 任意の 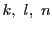 について
について
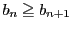 (等号は
(等号は
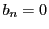 のときに限る) が成立する.
のときに限る) が成立する.
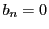 となる
となる  が存在しないとすると,
すべての
が存在しないとすると,
すべての 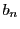 は自然数でしかも
は自然数でしかも
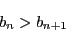
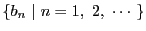 に最小値が存在しないことになり,
自然数の部分集合にはつねに最小値が存在するという,自然数の基本性質と矛盾する.
よって
に最小値が存在しないことになり,
自然数の部分集合にはつねに最小値が存在するという,自然数の基本性質と矛盾する.
よって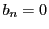 となる
となる  が存在する.
が存在する.
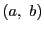 で
で  と
と  の最大公約数を表すことにする.
の最大公約数を表すことにする.
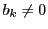 のとき
のとき
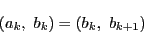
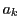 を
を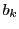 で割った商を
で割った商を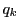 とおくと,
とおくと,
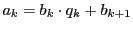 とかける. これから
とかける. これから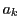 と
と 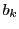 の公約数は
の公約数は 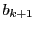 の
約数になり,
の
約数になり,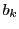 と
と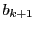 の公約数である.
の公約数である.
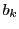 と
と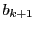 の公約数で最大のものが最大公約数
の公約数で最大のものが最大公約数
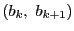 である.
ゆえに
である.
ゆえに
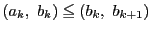 .
また
.
また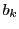 と
と 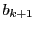 の公約数は
の公約数は 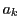 の約数になる.
同様に考え
の約数になる.
同様に考え
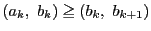 である.
である.
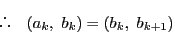
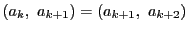 .
(3)からある自然数
.
(3)からある自然数 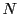 で
で
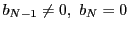 となるものがある.このとき
となるものがある.このとき
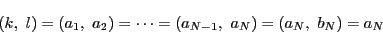
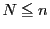 の
の  で同様の等式が成り立つので題意が示された.
で同様の等式が成り立つので題意が示された.
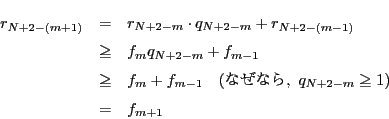
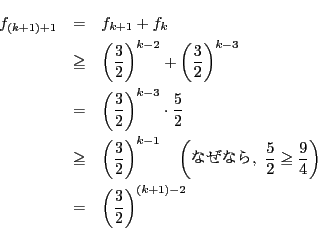
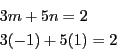
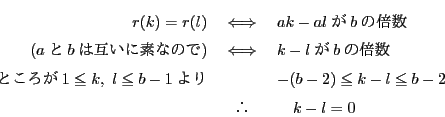
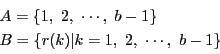
 (1)から
(1)から
 上には格子点がないので,この直線が
上には格子点がないので,この直線が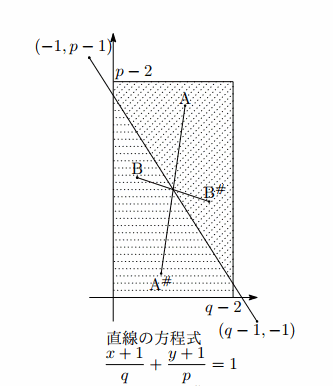
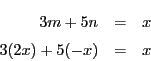
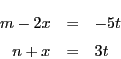
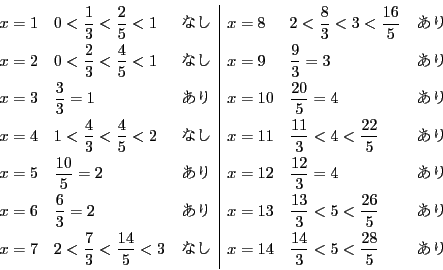
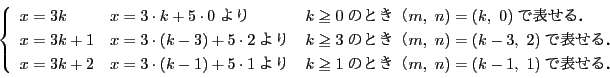
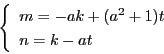
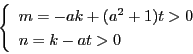

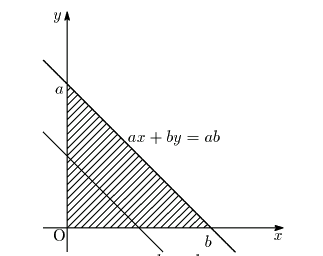
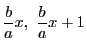 が整数となるのは
が整数となるのは 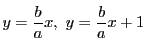 なので,
なので,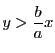 にあるので,
にあるので,
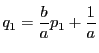 より,
より,
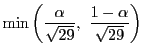 の
最大値以上に
の
最大値以上に  で
で 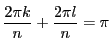 のときのみ.
のときのみ.
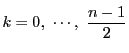 に対して
に対して 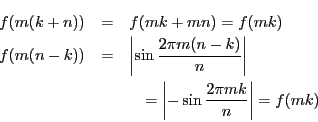

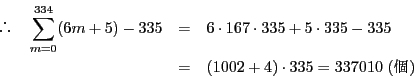
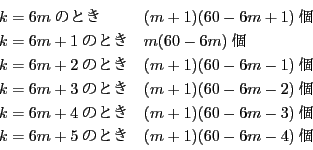
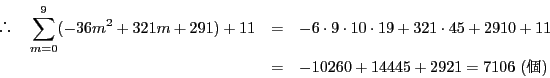
![\begin{displaymath}
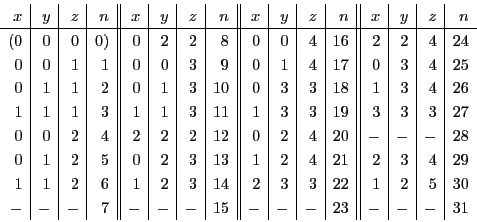
\begin{array}{lll}
f(k)=1となるkは& \left[\dfrac{50}...
...るkは& \left[\dfrac{50}{2^5} \right]&=1\ 個
\end{array}
\end{displaymath}](images/img3668.gif)
![\begin{eqnarray*}
S_n&=&1\cdot \left( \left[\dfrac{2^l}{2} \right]
- \left[\...
...right]\\
&=&2^{l-1}+2^{l-2}+\cdots+1=\dfrac{2^l-1}{2-1}=n-1
\end{eqnarray*}](images/img3671.gif)
![\begin{eqnarray*}
S_n&=&1\cdot \left( \left[\dfrac{n}{2} \right]
- \left[\df...
...-\dfrac{1}{2}}
<\dfrac{n}{2}\cdot\dfrac{1}{1-\dfrac{1}{2}}=n
\end{eqnarray*}](images/img3673.gif)
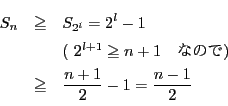

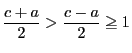 なので,
なので,
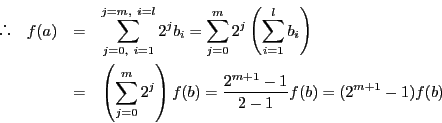
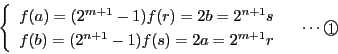
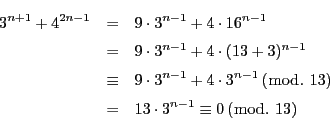
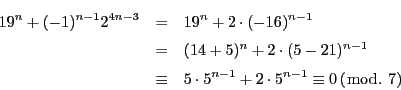
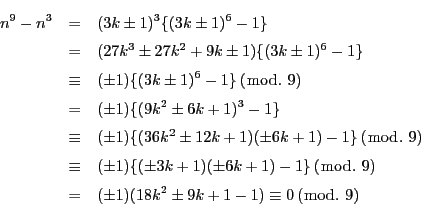
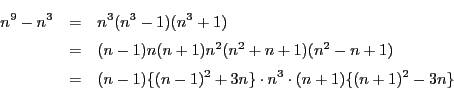
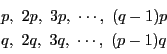
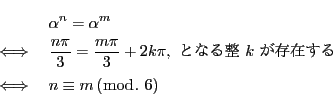
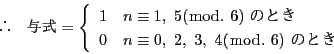
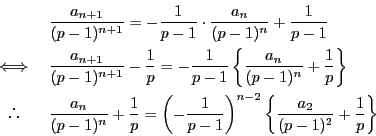
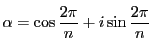 とおく.
とおく.
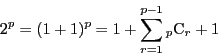
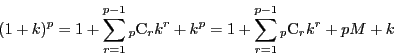
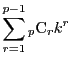 は
は
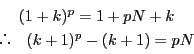
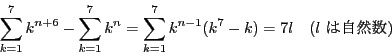
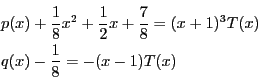
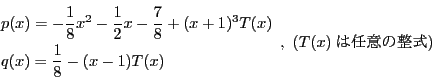
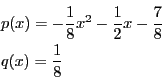
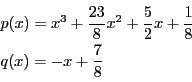
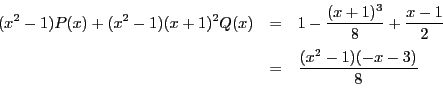
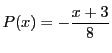 .
.
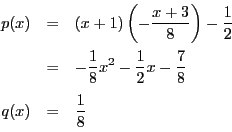
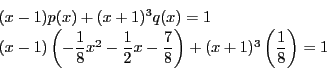
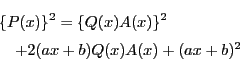
![\begin{eqnarray*}
&&Q(x)\left[B(x)-Q(x)\{A(x)\}^2\right.\\
&&\quad\left.-2(ax+b)A(x)\right]=(ax+b)^2
\end{eqnarray*}](images/img3962.gif)
 を持つ.
を持つ.
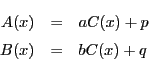
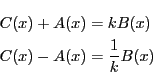
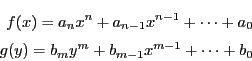
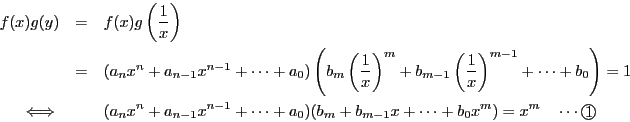
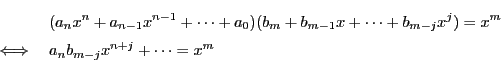
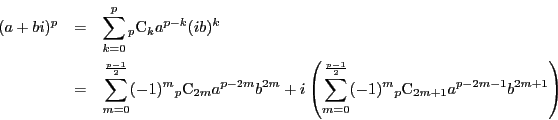
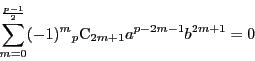
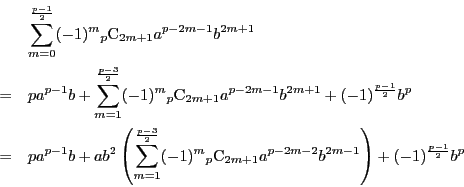
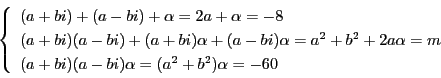
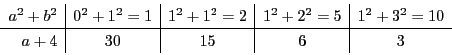
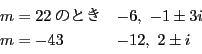
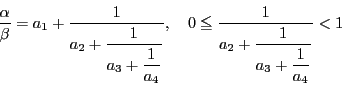
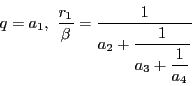
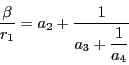
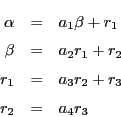
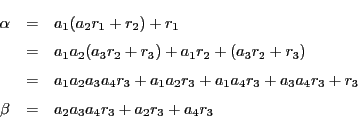
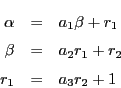
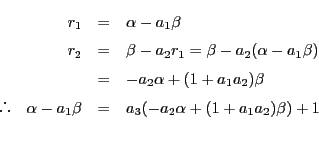
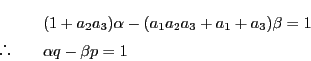
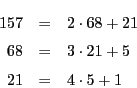
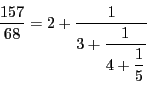
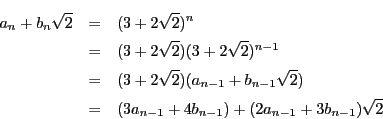
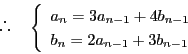
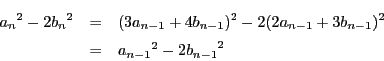
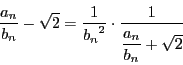
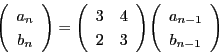
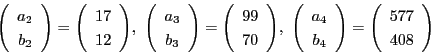
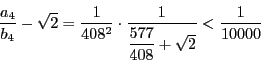
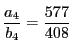
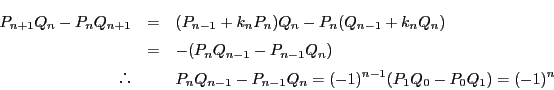
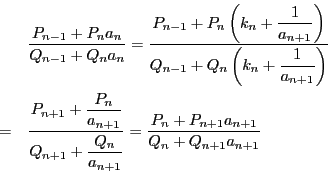
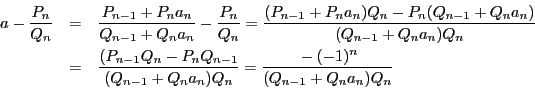
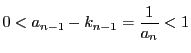 から
から 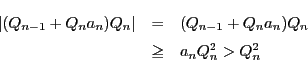
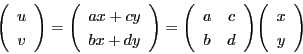
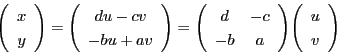
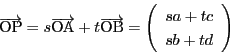
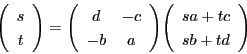
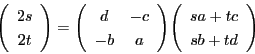
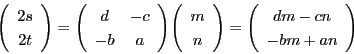
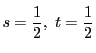 .
.
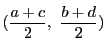 である以外になく,
これは平行四辺形の対角線の交点である.
である以外になく,
これは平行四辺形の対角線の交点である.
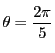 とすると,
とすると,
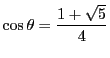 .ゆえに
.ゆえに
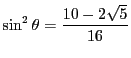 .これは無理数であり,したがって
.これは無理数であり,したがって
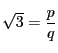 となる整数
となる整数 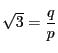 とおく.ここで
とおく.ここで