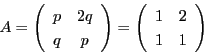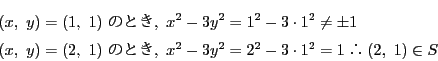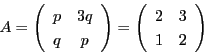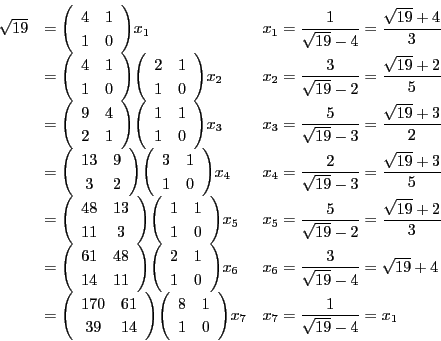次: 入試問題解答
上: 解答
前: 解答
次: 入試問題解答
上: 解答
前: 解答
解答 5 (問題
5)
[前半]
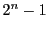 が素数なら,その約数は
が素数なら,その約数は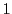 と
と 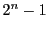 .
. 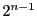 の約数は
の約数は
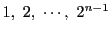 .したがって
.したがって  の約数は
の約数は
これらの和は
したがって真の約数の和はここから

を引いて

に等しい.
[後半](オイラーの解法)
 を偶数の完全数とする.
を偶数の完全数とする.
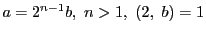 とおける.
とおける.
 は完全数なので
は完全数なので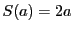 である.一方練習問題1-(4)から
である.一方練習問題1-(4)から
したがって
ゆえに
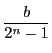
は整数である.
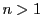
より
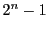
は

よりも小さい

の約数である.
つまり

のすべての約数の和
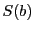
が

の二つの異なる約数の和になる.
したがって

は二つの約数しかもたない.つまり

は素数で,
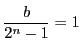
である.
よってまた
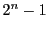
は素数である.
解答 6 (問題
6)
- (1)
-
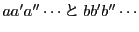 が互いに素でないとしてその最大公約数を
が互いに素でないとしてその最大公約数を
 とする.
とする.
 の素因数
の素因数  をとる.
をとる.  は
は
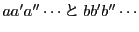 の公約数である.
したがって
の公約数である.
したがって  は
は
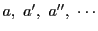 のいずれか,
のいずれか,
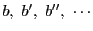 のいずれかの約数である.
のいずれかの約数である.
これは
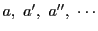 がおのおの
がおのおの
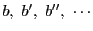 と
互いに素であることと矛盾する.
と
互いに素であることと矛盾する.
- (2)
-
とする.
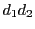 は
は 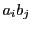 のすべての約数なので
のすべての約数なので 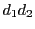 は
は 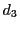 の約数.
の約数.
一方,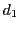 も
も 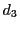 の約数なので
の約数なので 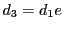 とおく.
とおく. 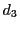 は
は
の約数で
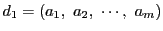 なので,
なので, 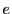 は
は 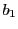 の約数.
各
の約数.
各 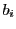 について言えるので
について言えるので 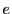 は
は
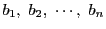 の公約数.
つまり
の公約数.
つまり 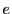 は
は 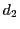 の約数.
の約数.
ゆえに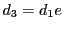 は
は 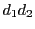 の約数.
の約数.
- (3)
-
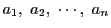 の任意の公約数に現れる素因数は
の任意の公約数に現れる素因数は
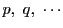 以外にはない.ゆえに公約数は
以外にはない.ゆえに公約数は
とおける.ここで
となり,最大公約数のときに限り
同様に,最小公倍数はその最小性により現れる素因数は
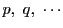 以外にはない.
ゆえに次の数
以外にはない.
ゆえに次の数
が公倍数なら
となり,最小倍約数のときに限り
- (4)
- (i)
- 各
 に対し
に対し
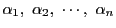 を並べ替えて
を並べ替えて
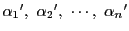 とおく.すると(3)より
とおく.すると(3)より
以下同様に
したがって,
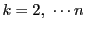 に対して
に対して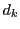 は
は 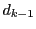 で割りきれる.
で割りきれる.
- (ii)
-
であるから
- (iii)
- また
- (iv)
-
なので(3)から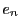 は
は
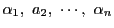 の
最小公倍数に等しい.
の
最小公倍数に等しい.
- (5)
-
とおけば,問題の等式を素因数  に指数で見ることにより,
に指数で見ることにより,
を示せばよい.
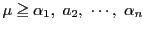 なら左辺は
なら左辺は
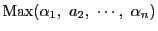 .右辺も同じ.
.右辺も同じ.
次に例えば
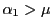 とする.
とする.
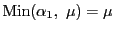 で,
で,
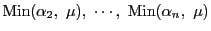 は
は 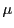 以下でから左辺は
以下でから左辺は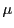 .
.
一方
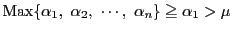 より,
右辺も
より,
右辺も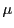 になる.
になる.
- (6)
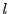 の素因数分解を
の素因数分解を
とする.
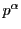 は
は
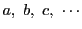 の少なくとも一つに含まれている.
の少なくとも一つに含まれている.
 を因子に含む
を因子に含む
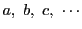 うち,
べき指数が最高のものが含まれている
うち,
べき指数が最高のものが含まれている
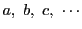 を指定する.
同じ指数のものがあるときはそのうちのいずれかをとる.
を指定する.
同じ指数のものがあるときはそのうちのいずれかをとる.
 が指定された
が指定された に含まれる最高べき因子の積を
に含まれる最高べき因子の積を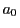 とする.
とする.
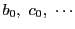 をそれぞれ同様に定める.
このとき
をそれぞれ同様に定める.
このとき
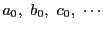 のどの2つも互いに素で
のどの2つも互いに素で
である.
解答 7 (問題
7)
前半は後半の
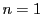
の場合なので,後半を示せばよい.
つまり
ここで
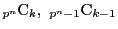
は組合せの場合の数なので正の整数である.
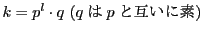 とおくと
とおくと
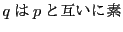
なので
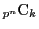
が
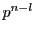
の倍数である.
解答 8 (問題
8)

に現れる素数

の最高べきの指数を
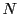
とする.
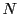
は
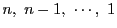
に含まれる素数

の個数に等しい.
とする.
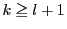
なら
![$\left[\dfrac{n}{p^k}\right]=0$](images/img2999.gif)
である.
解答 9 (問題
9)
(i)既約分数 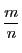 が部分分数に分解できること.
が部分分数に分解できること.
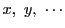 に関する条件を考えなければ
に関する条件を考えなければ
は
となり,これは
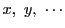
に関する一次不定方程式で
係数は互いに素なので定理
5によって解を持つ.
ここで  を
を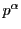 で割って
で割って
となったとすれば
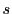
を調整して

の代わりに

を用いることで条件
にできる.
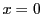
ならその項はいらないので,
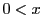
としてよい.
したがって題意を満たす部分分数分解が存在する.
(ii)部分分数分解の一意性を示す.
二つの分解
があれば辺々引いて
両辺に

をかけて分母を払うと
となり
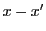
が
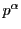
で割りきれる.しかし
なので(一方に現れない項が他方に現れる可能性を考え等号が付いている),
ゆえに
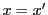
.同様に
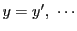
.その結果
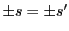
.
解答 14 (問題
14)
- (1)
-
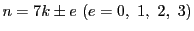 とおく.
とおく.
- (2)
-
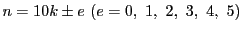 とおく(5は二重になっている).
とおく(5は二重になっている).
- (3)
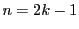 とおく.
とおく.
- (4)
-
解答 15 (問題
15)
- (1)
-
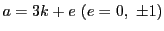 に対して
に対して
である.
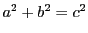 となる整数
となる整数 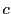 が存在するなら右辺は3を法として0か1に合同なので
が存在するなら右辺は3を法として0か1に合同なので
となることはできない.
ところが,左辺が
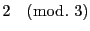 になるのは
になるのは 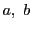 とも
3の倍数でないときである.これが否定されるので題意が示された.
とも
3の倍数でないときである.これが否定されるので題意が示された.
- (2)
- 同様に
である.
ゆえに,1と4をどのように加えても5を法として1や4に合同にはならない.
つまり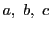 のうち少なくとも
のうち少なくとも 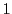 つは
つは 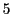 の倍数である.
の倍数である.
解答 17 (問題
17)
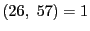
なので解が存在する.
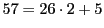
より
ゆえに解があれば 11 に 57 を法として合同である.
解が存在することは分かっているので
別解
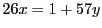 となる整数
となる整数 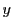 があればよい.
があればよい.
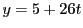
とおくと
解答 18 (問題
18)
つまり
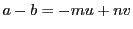
となる整数解
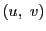
が存在することと同値である.
これは
と同値である(定理
5).
二つの解 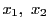 が存在したとする.このとき
が存在したとする.このとき
つまり 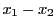 は
は  と
と  の最小公倍数
の最小公倍数 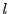 で割り切れる(定理2).
で割り切れる(定理2).
解答 19 (問題
19)
必要性は明らかである.よって,条件が成立しているとする.
ここで
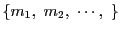 で
で
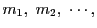 の最小公倍数を表す.
すると前問から
の最小公倍数を表す.
すると前問から
の解を
のように表すことができる.これに第三の合同式を組合わせて
この解が
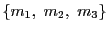
を法としてただ一つに定まることを示す.
仮定から
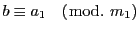 .
ゆえに
.
ゆえに
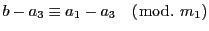 .
すなわち
.
すなわち
同様に
つまり
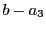
は
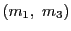
かつ
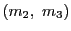
で割りきれ,したがって
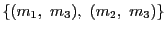
で割りきれる.
であるから(練習問題
6の(5)),前問により

は
に関してただ一つ定まる.
順次この操作を繰りかえすことにより題意が示された.
解答 20 (問題
20)
- (1)
-
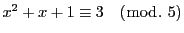 を解く.
を解く.
これを用いて解く.
- (2)
-
は四つの解をもつ.それらは,
から求められる.
解答 21 (問題
21)
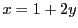
を奇数とする.
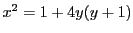
で
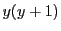
は偶数だから,
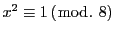
.
ゆえに
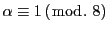 は
は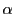 が奇数であるときに問題の合同式が解をもつための必要条件である.
が奇数であるときに問題の合同式が解をもつための必要条件である.
このとき題意を 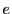 に関する数学的帰納法で示す.
に関する数学的帰納法で示す.
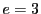 のとき.
のとき.
解は
である.このいずれを
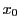
としても,この4数は
となっており,解の存在とその形に関して題意が成立している.
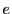 のときの成立を仮定して
のときの成立を仮定して 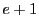 のときの成立を示す.
のときの成立を示す.
つまり
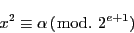 |
(9.1) |
の解は四つあり,そのうちの一つを
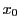
とすれば4解は
と表されることを示す.
さて,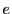 のときの解
のときの解 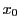 を用いれば
を用いれば 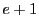 のときの解は
のときの解は
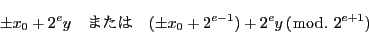 |
(9.2) |
の形をしていなければならない.
そして(
9.2)が(
9.1)を満たさなければならないので
のいずれかが成立する
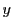
から
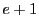
のときの解が求まる.
仮定から整数  を用いて
を用いて
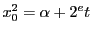 と表せる.
これを用いると(9.3)は
と表せる.
これを用いると(9.3)は
となり,これは

が奇数ならつねに成立せず,

が偶数ならつねに成立する.
次に(9.4)について.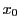 は奇数で
は奇数で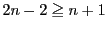 であるから
であるから
よって(
9.4)は
となる.これは

が偶数ならつねに成立せず,

が奇数ならつねに成立する.
つねに成立するとき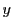 は任意なので,
は任意なので,
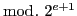 に関しては
に関しては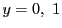 をとることができる.
をとることができる.
よって が偶数なら
が偶数なら
の四つが解である.
 が奇数なら
が奇数なら
の四つが解である.
以上によって,数学的帰納法により題意が示された.
解答 22 (問題
22)
- (1)
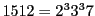 であるから
であるから
実際
である.
- (2)
 が1512と互いに素なら
が1512と互いに素なら 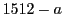 も1512と互いに素である.
したがって1512と互いに素なものを小さい順にならべると
も1512と互いに素である.
したがって1512と互いに素なものを小さい順にならべると
となる.  と
と 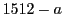 を組にするとそれらの和は
を組にするとそれらの和は
解答 23 (問題
23)
点
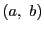
と点
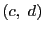
および原点が同一直線上にあるのは
となるときである.つまり一方の分子分母を約分して他方になるときである.
したがって,領域 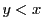 の中にあって題意をみたす点
の中にあって題意をみたす点 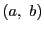 は
既約分数
は
既約分数
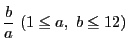 の個数である.
分母を
の個数である.
分母を  に対して
に対して 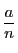 が既約なものは
が既約なものは 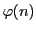 個ある.
個ある.
直線 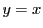 上では
上では 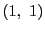 のみが題意をみたす.
のみが題意をみたす.
解答 24 (問題
24)
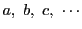
と与えられた互いに素な数の個数に関する
数学的帰納法で証明する.
 がただ一つ与えられたときは
がただ一つ与えられたときは
![$1,\ 2,\ \cdots,\ [x]$](images/img2632.gif) のなかで
のなかで  の倍数は
の倍数は
だけある.
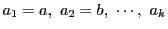 が与えられたときそれらのいずれでも
割り切れない数の個数を
が与えられたときそれらのいずれでも
割り切れない数の個数を 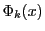 とし,これについては成立しているとする.
とし,これについては成立しているとする.
さらに 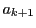 が追加されたとする.
このときは,さらに
が追加されたとする.
このときは,さらに 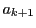 の倍数
の倍数
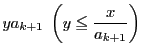 を除かなければならない.そのうち
を除かなければならない.そのうち 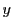 が
が
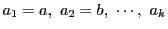 で割り切れるものは
すでに除かれているので,新たに除くべきものは
で割り切れるものは
すでに除かれているので,新たに除くべきものは
個ある.
ゆえに 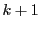 のときも成立し,題意が示された.
のときも成立し,題意が示された.
解答 25 (問題
25)
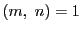
ならば,
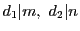
とすれば
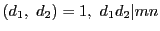
.
逆に, 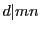 なら
なら
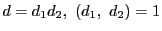 の形に書ける.
の形に書ける.
注意 9.1.1
これを用いれば,補題
2の別の証明ができる.
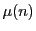 は明らかに乗法的関数である.
は明らかに乗法的関数である.
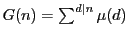 で
で 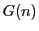 を定めると
を定めると
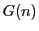 も乗法的関数である.
ゆえに
も乗法的関数である.
ゆえに
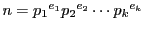 のとき
のとき
ところが
ゆえに補題が示された.
解答 26 (問題
26)
1から
![$[nx]$](images/img3130.gif)
までの整数のうち,

との最大公約数が

であるものは
と書ける.ところが
であるからその個数は1から
![$\left[\dfrac{nx}{d}\right]$](images/img3133.gif)
までの整数のうち,
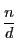
と互いに素であるものの個数
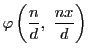
に等しい.1から
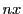
を超えない最大の整数までの整数は
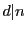
に関して1度ずつ
数えられるので,

が

の正の約数を動けば
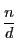
の正の約数をすべて動くので第一式が示された.
第二式は第一式よりメビウスの反転公式で得られる.
解答 27 (問題
27)
であり,
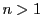
のとき
であるから,
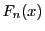
の定数項は
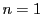
の場合以外
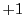
である.
解答 28 (問題
28)
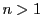
のときすべての

乗根の和は,
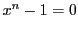
から0である.
従って原始

乗根の和を
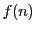
をおくと,
整数

と

に関する等式と見ればメビウスの反転公式(6節)から
解答 29 (問題
29)
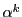
はもちろん

乗根である.
であるが,
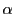
が原始

乗根なのでこれは
を意味する.従って

を

に関する剰余系にとった
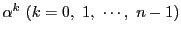
はすべて異なる.
つまりこれらが,1の

乗根のすべてである.
つぎに
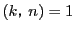
なら,
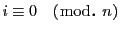
が結論されるので,
このとき
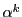
は原始

乗根である.このような

は
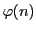
個ある.
定理
21 から原始

乗根はちょうど
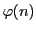
個なので,
これらが原始

乗根のすべてである.
解答 30 (問題
30)
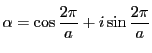
,
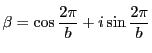
とおく.整數
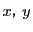
に対して
となる.
定理
17(6節)の証明にあるように,
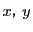
に
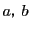
を法とする剰余系の値を与えれば
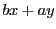
は
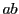
を法とする剰余系になり,
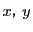
に
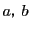
を法とする既約剰余系の値を与えれば
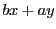
は
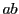
を法とする既約剰余系になる.
解答 31 (問題
31)
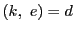
とおき,
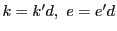
とする.
逆に
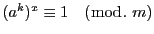
とする.このとき定理
24から
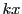
は
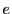
の倍数である.このとき
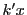
が
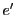
の倍数になる.
ところが
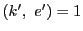
だから

は
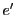
の倍数である.
ゆえに
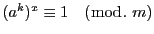 となる最小の
となる最小の
 が
が
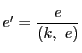 である.
である.
注意 9.1.2
例(3)(4)については『めざせ,数学オリンピック』(J.コフマン,現代数学社)
にいくつかの計算例が載っている.
それを紹介する.
20以下の素数  について
について 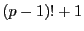 を計算する.
を計算する.
20以下の について
について 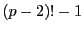 を計算する.
を計算する.
解答 33 (問題
33)
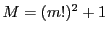
とおく.
は
で割り切れないので
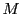
の1でない因数はすべて

より大きい.
そこで
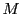
が
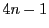
型の素因数

をもったとする.
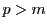
である.
フェルマの小定理から
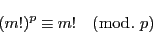 |
(9.5) |
次に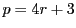 とおき,因数分解
とおき,因数分解
を
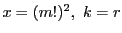
で用いる.このとき
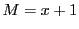
であるから
因数分解は
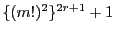
が
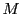
で割り切れることを示している.
一方,
である.
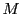
で割り切れるならその素因数

でも割り切れる.
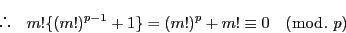 |
(9.6) |
(9.5), (9.6)から
これは
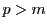
と矛盾した.
ゆえに
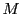
は
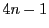
型の素因数はもたない.つまりすべての素因数は
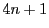
型の素数である.
任意の自然数  に対して,
に対して,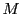 の素因数
の素因数  は必ず存在し(
は必ず存在し(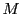 自身が素数なら
自身が素数なら 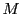 ,
,
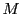 が合成数なら
が合成数なら 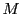 の素因数),
の素因数), は
は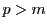 である
である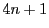 型の素数になる.
つまり任意の自然数
型の素数になる.
つまり任意の自然数  に対してそれより大きい
に対してそれより大きい 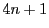 型の素数がつねに存在するので
型の素数がつねに存在するので
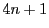 型の素数は無数に存在する.
型の素数は無数に存在する.
解答 34 (問題
34)
10 の法 91 に対する指数 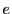 は 6 である.
は 6 である.
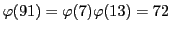 であるから分母が91の既約真分数は72個ある.
であるから分母が91の既約真分数は72個ある.
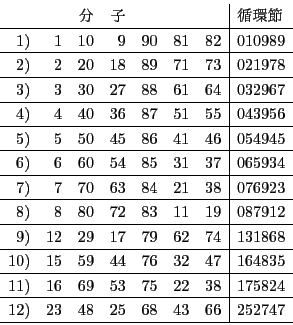
したがって,72個の分数が6個ずつ12の循環節が等しい群に分かれる.
これから次の循環小数ができる.
分子と循環節は次の通り.
解答 38 (問題
38)
ところが

は原始根なので
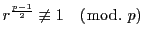
.
ゆえに
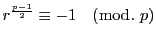
.
つまり題意が示された.
解答 40 (問題
40)
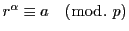
とおく.
さらに
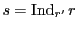
,つまり
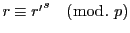
とおく.あわせて
両辺
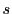
で割って題意の式を得る.
解答 41 (問題
41)

を法

の原始根とすれば

が
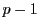
で割りきれないので二つの集合
の各元は互いに

を法として合同の関係で一対一に対応している.ゆえに
ここで分子は
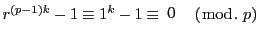
,
分母は
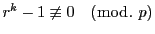
であることに注意する.
解答 44 (問題
44)
ここで
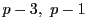
は隣り合う二つの偶数なのでともに4の倍数になることはない.
ゆえに
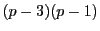
が16の倍数になるのは
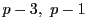
のいずれかが8の倍数になるときにかぎる.
解答 45 (問題
45)
相互法則から
ところが法5については
なので
-
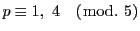 のとき
のとき
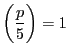
-
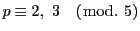 のとき
のとき
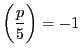
となり,あわせて題意が示された.
解答 46 (問題
46)
相互法則から

を 3, 4, 12 を法とする剰余で分類して値を決める.
したがって確かに題意が成立している.
解答 47 (問題
47)
で
となる
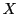
は二つしかないので

を法として,
はちょうど二つずつが同じになる.
したがって
のうち半分が平方剰余で半分が非剰余である.
ところが第一補充法則から
したがって
また

と
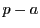
の偶数奇数は逆なので
となり,これはともに0である.
注意 9.1.3
これはガウス環を用いてピタゴラス数の一般解を求めるものである.
解答 50 (問題
50)
3次方程式の他の解は実数なのでこれを
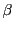
とおく.解と係数の関係から
となる.これを整理して
である.
まず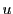 がある整数
がある整数 を用いて
を用いて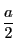 と表せること示す.
第2式から
と表せること示す.
第2式から
ここに第1式,第3式を用いて
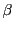
と
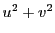
を消去する.
整理して
ここで有理数
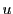
を互いに素な整数

と

を用いて
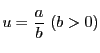
とおく.
方程式に代入して
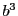
を乗じ一部移項する.
右辺は

の倍数である.
左辺も

の倍数であるが
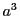
と

は互いに素なので,
8が

の倍数,つまり

が8の約数となることが必要である.
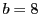 なら代入して8で割ると
なら代入して8で割ると
これから

が偶数となり

と

が互いに素に反する.
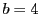 なら代入して8で割ると
なら代入して8で割ると
これから

が偶数となり

と

が互いに素に反する.
よって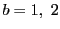 .つまり
.つまり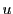 は整数
は整数 を用いて
を用いて
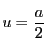 とおける.
とおける.
この結果,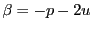 が整数となりさらに
が整数となりさらに
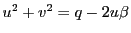 も整数である.
も整数である.
なので有理数
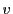
も整数
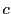
を用いて
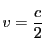
とおける.そして
が整数.
そのためには分子が偶数でなければならないので
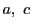
がともに偶数かともに奇数であることが必要.
ともに奇数の場合
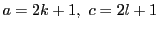
とすると
となり
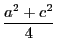
が整数でない.
よって も
も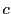 も偶数となり,その結果
も偶数となり,その結果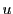 と
と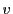 が整数となる.
が整数となる.
注意 9.1.4
ガウスによる有理整数係数の多項式に関する定理:
整数係数多項式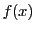 が有理数の範囲で因数分解されれば,
有理整数の範囲で因数分解される.
が有理数の範囲で因数分解されれば,
有理整数の範囲で因数分解される.
を用いると,
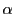
が
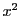
の係数が1の
有理整数係数の二次方程式の根であることがわかる.
この二次方程式を
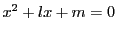
とおくと,
となる.これから
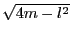
が整数とならねばならず,
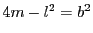
とおく.

が奇数とすると
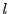
も奇数であるが,このとき両辺4で割った余りが異なるので,これはない.かくして
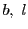
が偶数となり,
題意が示される.
注意 9.1.5
最高次の項の係数が1である整数係数の代数方程式の解となる数を
「(代数的)整数」と呼ぶ.
ガウス整数
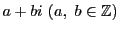
は
二次方程式
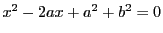
の解なので代数的整数である.
ガウス整数環に対してその商環
は体である.ガウス商体といおう.これは分母を実数化することで
と同じものになる.
本問はガウス商体の元で代数的整数であるものの集合は,
ちょうどガウス整数環になることを示している.
代数的整数の理論が19世紀末から20世紀にかけて大発展した.
『数論初歩』に引き続く分野である.
高木貞治はこの分野で「類体論」と呼ばれる決定的な仕事をした.
解答 52 (問題
52)
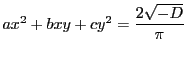
はちょうど面積が4の楕円である.
これについては『数学対話』「三角形に辺の中点で内接する楕円(シュタイナー楕円)」の
なかの「一次変換」参照のこと.ゆえにミンコフスキーの定理より領域
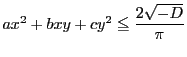
には原点以外の格子点が含まれる.
解答 53 (問題
53)
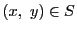 かつ
かつ 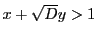 であるものの中で最小の元を確定させなけ
ればならない. そこで, まず
であるものの中で最小の元を確定させなけ
ればならない. そこで, まず
を示す.
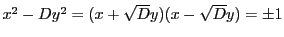 より,
より,
したがって,
となる. すると, 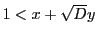 ,
,
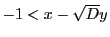 より,
より,
また, 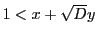 ,
,
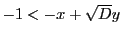 より,
より,
以上より, 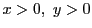 という条件のもとで,
という条件のもとで, 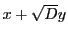 の値が最小と
なるものを考 えればよい.
の値が最小と
なるものを考 えればよい.
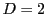 のとき,
のとき,
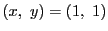 に対して,
に対して,
となり, 上の考察と合わせると, これが求めるものである. この場合,
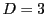 のとき,
のとき,
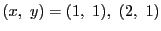 に対して,
に対して,
となり, 上の考察と合わせると,
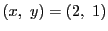 が求めるものである.
この場 合,
が求めるものである.
この場 合,
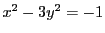 の解があれば,
の解があれば,
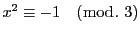 となる
となる  が存在することになるが, オイラーの規準より
が存在することになるが, オイラーの規準より
なので,法3に関して 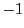 は平方剰余ではないので,そのような解はない.
は平方剰余ではないので,そのような解はない.


 次: 入試問題解答
上: 解答
前: 解答
Aozora Gakuen
次: 入試問題解答
上: 解答
前: 解答
Aozora Gakuen
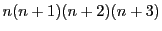 は4連続数だから,
この4個の整数の中には2の倍数が2個あり,
そのうち一方は4の倍数.また3の倍数が少なくとも1個ある.
ゆえにこれは24の倍数である.
は4連続数だから,
この4個の整数の中には2の倍数が2個あり,
そのうち一方は4の倍数.また3の倍数が少なくとも1個ある.
ゆえにこれは24の倍数である.
 が奇数なので,
が奇数なので, 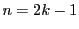 とおく.
とおく.
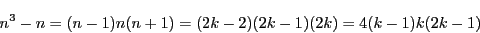
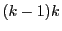 は2連続数なので偶数.
ゆえに
は2連続数なので偶数.
ゆえに 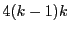 は8の倍数.あわせて24の倍数であることが示せた.
は8の倍数.あわせて24の倍数であることが示せた.
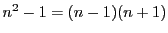 である.
である.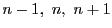 のなかには3の倍数があるが,
のなかには3の倍数があるが,
 が3で割り切れないので,
が3で割り切れないので, 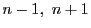 のいずれかは3の倍数である.
また(2)と同様に
のいずれかは3の倍数である.
また(2)と同様に 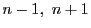 のいずれかは4の倍数で他方も2の倍数である.
ゆえに
のいずれかは4の倍数で他方も2の倍数である.
ゆえに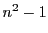 は24の倍数である.
は24の倍数である.
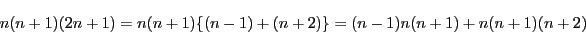
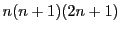 は6の倍数である.
は6の倍数である.
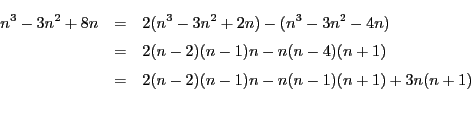
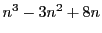 は6の倍数である.
は6の倍数である.
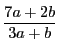 は既約分数である.
は既約分数である.
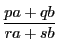 は既約分数である.
は既約分数である.
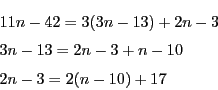


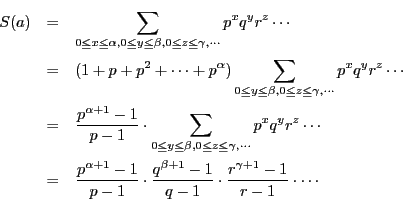
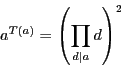
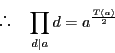
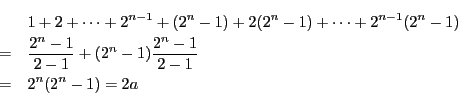
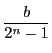 は整数である.
は整数である. 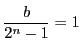 である.
よってまた
である.
よってまた 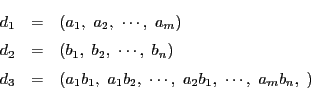
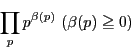
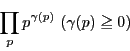
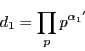
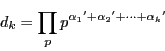
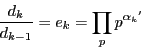
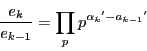
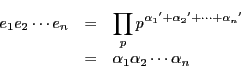
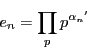
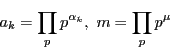
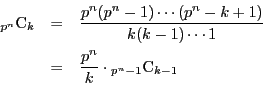
![$\left[\dfrac{n}{p^k}\right]=0$](images/img2999.gif) である.
である.
![\begin{displaymath}
\begin{array}{ll}
n,\ n-1,\ \cdots,\ 1 のなかでちょ...
...のの個数は
&\left[\dfrac{n}{p^l}\right]
\end{array}
\end{displaymath}](images/img3000.gif)
![\begin{eqnarray*}
∴\quad N&=&1\cdot \left(\left[\dfrac{n}{p}\right]
-\left...
...}\right]\\
&=&\sum_{k=1}^{\infty}\left[\dfrac{n}{p^k}\right]
\end{eqnarray*}](images/img3001.gif)
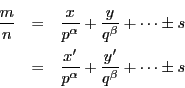
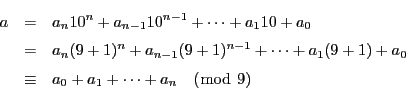
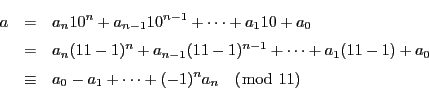

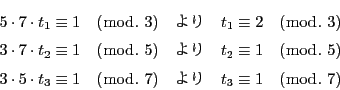
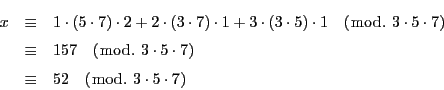
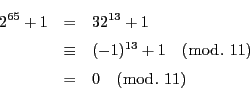
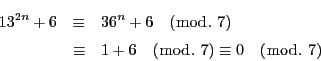
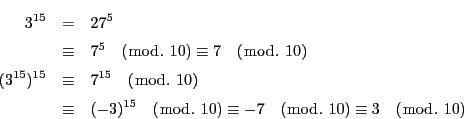
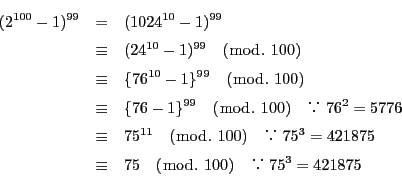
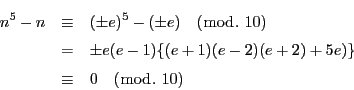
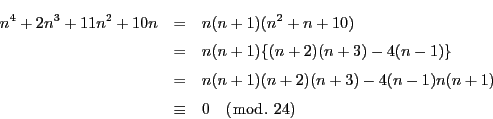
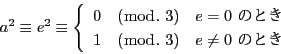
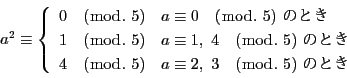

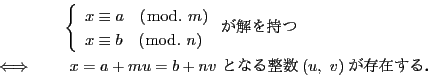
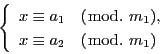
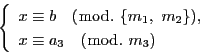
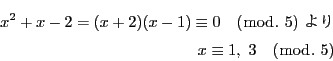
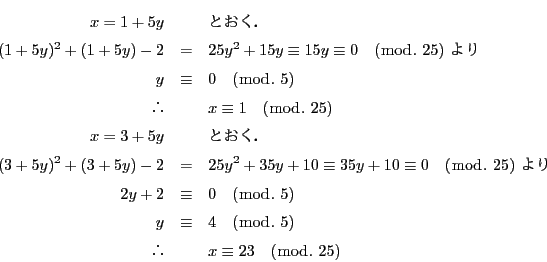
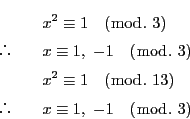
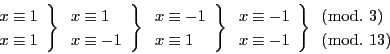
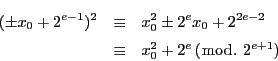
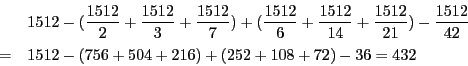
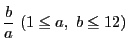 の個数である.
分母を
の個数である.
分母を 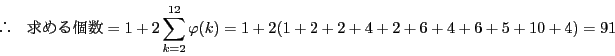
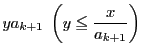 を除かなければならない.そのうち
を除かなければならない.そのうち ![\begin{eqnarray*}
∴\quad \Phi_{k+1} (x)&=&\Phi_k (x)-\Phi_k \left(\dfrac{x}{...
...ght]- \cdots
-\left[\dfrac{x}{a_1a_2a_{k+1}}\right]- \cdots
\end{eqnarray*}](images/img3120.gif)
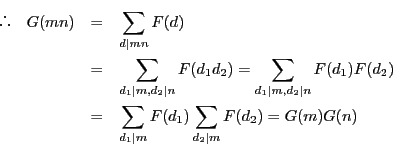
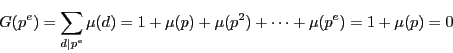
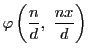 に等しい.1から
に等しい.1から ![\begin{displaymath}[nx]=\sum_{d\vert n}\varphi\left(\dfrac{n}{d},\ \dfrac{nx}{d} \right)
\end{displaymath}](images/img3136.gif)
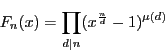
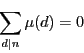
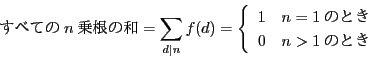
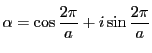 ,
,
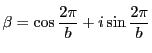 とおく.整數
とおく.整數 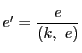 である.
である.


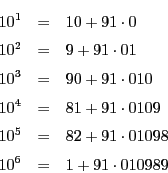
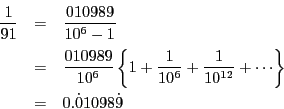
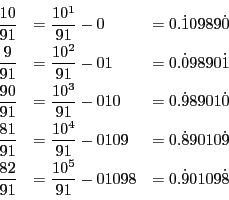
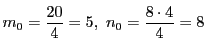 とする.
とする.
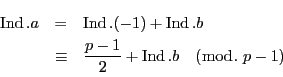
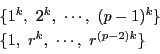
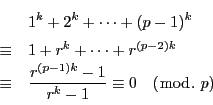
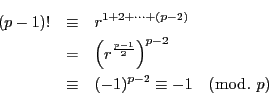

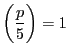
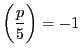
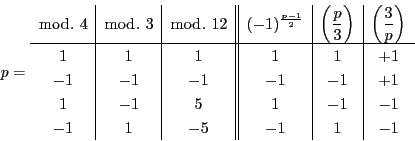
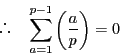
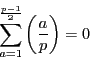
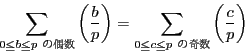
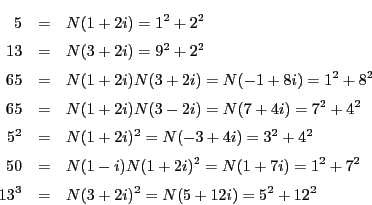
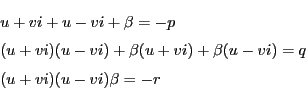
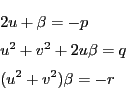
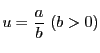 とおく.
方程式に代入して
とおく.
方程式に代入して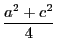 が整数でない.
が整数でない.
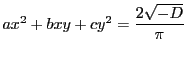 はちょうど面積が4の楕円である.
これについては『数学対話』「三角形に辺の中点で内接する楕円(シュタイナー楕円)」の
なかの「一次変換」参照のこと.ゆえにミンコフスキーの定理より領域
はちょうど面積が4の楕円である.
これについては『数学対話』「三角形に辺の中点で内接する楕円(シュタイナー楕円)」の
なかの「一次変換」参照のこと.ゆえにミンコフスキーの定理より領域
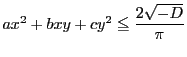 には原点以外の格子点が含まれる.
には原点以外の格子点が含まれる.