したがって指数を次のように定義することもできる.
![]() を
を ![]() の原始根とすれば
の原始根とすれば ![]() を法とする0でない任意の剰余系の
代表である整数
を法とする0でない任意の剰余系の
代表である整数 ![]() に対して
に対して
意味が明白なときは等号で表す.また「![]() の値」というときは,厳密には
の値」というときは,厳密には ![]() を法とする剰余系の一つを指すが,その剰余系のある代表値で表すこともする.
底が定まっているときは省略して
を法とする剰余系の一つを指すが,その剰余系のある代表値で表すこともする.
底が定まっているときは省略して![]() とも記すことにする.
とも記すことにする.
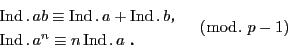
『初等整数論講義』によれば,Jacobi は『Canon arithmeticus』(1839)において 1000 以下の 素数を法とする指数を計算している.Jacobi は計算を楽しんだのだろう.そして Cunninghana という人がこの Jacobi の表の検算をおこない,正誤表が数学雜誌 「Messenger of methematics, 46巻」(1916)に載っているそうである.
指数の理論の応用として,合同方程式の解の存在に関する次の定理を得る.
証明
![]() を解くには
を解くには
![]() を法とする原始根
を法とする原始根 ![]() をとって
をとって
逆に
![]() ならば,
ならば,
![]() .
ゆえに
.
ゆえに ![]() は
は ![]() で割りきれる.
つまり
で割りきれる.
つまり ![]() が
が ![]() で割りきれ,二項合同方程式は解をもつ.
解があるとき解の数は
で割りきれ,二項合同方程式は解をもつ.
解があるとき解の数は ![]() 個である.□
個である.□
この定理は今日では,有限群 ![]() がただ一つの元(原始根)で
生成される巡回群であること,およびその巡回群に関する二,三の補題で示される.
ここでは『初等整数論講義』にしたがって,整数論らしい証明をおこなっている.
がただ一つの元(原始根)で
生成される巡回群であること,およびその巡回群に関する二,三の補題で示される.
ここでは『初等整数論講義』にしたがって,整数論らしい証明をおこなっている.
合同方程式
![]() が解があるかないかにしたがって
が解があるかないかにしたがって
![]() を
を ![]() の 「
の 「![]() べき剰余」,または「非剰余」という.
もちろん,べき剰余か非べき剰余かは,同じ剰余系に属する二数では同じである.
つまりべき剰余か非べき剰余かは
べき剰余」,または「非剰余」という.
もちろん,べき剰余か非べき剰余かは,同じ剰余系に属する二数では同じである.
つまりべき剰余か非べき剰余かは ![]() を法とする剰余系に関することである.
0はつねに
を法とする剰余系に関することである.
0はつねに ![]() べき剰余である.
べき剰余である.
![]() である
である ![]() について言えば,
について言えば,
![]() のとき任意の
のとき任意の ![]() が
が ![]() べき剰余である.
べき剰余である.
![]() のときは,
のときは, ![]() が
が ![]() の倍数となる
の倍数となる ![]() だけが
だけが
![]() べき剰余である.
べき剰余である.
![]() とおけば,指数が
とおけば,指数が
![]() となる数が
となる数が ![]() べき剰余である.
したがって
べき剰余である.
したがって ![]() べき剰余は
べき剰余は ![]() を法として
を法として![]() 個の既約剰余類のなかの
個の既約剰余類のなかの
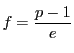 個だけある.
個だけある.
実際,既約剰余系