次: 相互法則
上: 剰余類
前: 指数
次: 相互法則
上: 剰余類
前: 指数
練習問題 11 (解答
11)
今日が金曜日であるとする. 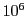 ,
, 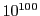 ,
, 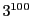 日後はそれぞれ何曜日か.
日後はそれぞれ何曜日か.
練習問題 12 (解答
12)
3で割れば1余り,5で割れば2余り,7で割れば3余る正で最小の整数を求めよ.
練習問題 18 (解答
18)
法 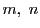 の最大公約数を
の最大公約数を 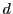 ,最小公倍数を
,最小公倍数を 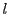 とする.
とする.
が解を持つ必要十分条件は
であることを示せ.
またこのとき,解は
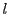
を法としてただ一つであることを示せ.
練習問題 19 (解答
19)
 個の合同方程式
個の合同方程式
が解を持つための必要十分条件は
であることを示せ.
このとき解は
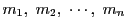
の最小公倍数を法としてただ一つであることを示せ.
練習問題 21 (解答
21)
『初等整数論講義』(高木貞治著),39ページ〔問題1〕より.
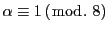 であるとする.このとき
であるとする.このとき 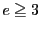 に対して
に対して
の
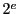
を法とする解は四つあり,その一つを
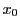
とすれば4解は
と表されることを示せ.
練習問題 22 (解答
22)
- (1)
- 1 から 1512 までの自然数で 1512 と互いに素なものはいくつあるか.
- (2)
- それらの和はいくらか.
練習問題 23 (解答
23)
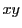 平面上,不等式
平面上,不等式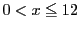 ,
,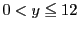 で定まる領域にある格子点を考える.
で定まる領域にある格子点を考える.
原点とこれらの格子点を結ぶ線分で,両端以外に格子点が乗っていないものは
何本あるか.
練習問題 24 (解答
24)
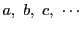 は二つずつ互いに素であるとし,
は二つずつ互いに素であるとし,
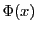 は実数
は実数 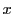 を超えない自然数のなかで
を超えない自然数のなかで
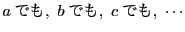 割り切れないものの個数を表すとする.
割り切れないものの個数を表すとする.
を示せ.ただし
![$[x]$](images/img1215.gif)
は
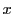
を超えない最大の整数を表す.
練習問題 25
(解答
25)
整数で定義された関数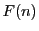 が乗法的関数のとき
が乗法的関数のとき
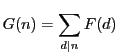 で定義された関数
で定義された関数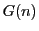 も乗法的関数であることを示せ.
また,この事実を用いて補題2の別証を考えよ.
も乗法的関数であることを示せ.
また,この事実を用いて補題2の別証を考えよ.
練習問題 26
(解答
26)
正の実数 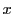 を超えない自然数のうちで
を超えない自然数のうちで  と互いに素であるものの
個数を
と互いに素であるものの
個数を
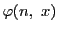 とおく.
とおく.
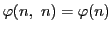 である.
である.
![$[x]$](images/img1215.gif) で
で 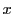 を超えない整数を表すと定理19,定理20の一般化として
を超えない整数を表すと定理19,定理20の一般化として
が成り立つことを示せ.
練習問題 29 (解答
29)
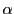 を1の原始
を1の原始  乗根とすれば
乗根とすれば
がすべての

乗根で,そのうち
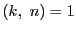
なる
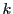
に対する
ものがちょうど原始

乗根になることを示せ.
以下の練習問題は,『めざせ,数学オリンピック』(J.コフマン,現代数学社)に教えられた.
練習問題 33 (解答
33)
因数分解
を活用して,任意の自然数
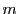
に対して
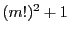
の素因数はすべて
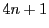
型の素数であることを示せ.
これから
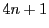
型の素数が無数にあることを示せ.
入試問題 22 (解答
22)
[82名古屋市大]
 を自然数とするとき,
を自然数とするとき,
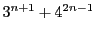 は13で割りきれることを証明せよ.
は13で割りきれることを証明せよ.
入試問題 23 (解答
23)
[東工大]
 を正の整数とするとき、
を正の整数とするとき、
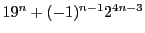 は、
は、 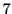 の倍数であることを示せ.
の倍数であることを示せ.
入試問題 24 (解答
24)
[82九大]
整数を係数とする  次の多項式
次の多項式
について次のことを証明せよ.
- (1)
- 有理数
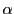 が方程式
が方程式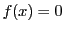 の1つの解ならば,
の1つの解ならば,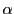 は整数である.
は整数である.
- (2)
- ある自然数
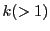 に対して,
に対して, 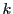 個の整数
個の整数
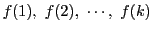 のどれもが
のどれもが 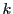 で割り切れなければ方程式
で割り切れなければ方程式 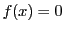 は有理数の解をもたない.
は有理数の解をもたない.
入試問題 25 (解答
25)
[01京大文系前期]
任意の整数  に対し,
に対し, 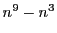 は9で割り切れることを示せ.
は9で割り切れることを示せ.
入試問題 27 (解答
27)
[70東大理系]
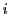 を虚数単位とし
を虚数単位とし
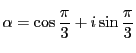 とおく.また
とおく.また  はすべての自然数にわたって動くとする.このとき
はすべての自然数にわたって動くとする.このとき
- (1)
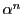 は何個の異なる値をとりうるか.
は何個の異なる値をとりうるか.
- (2)
-
の値を求めよ.
入試問題 29 (解答
29)
[01京都府立医大]
0でない複素数からなる集合 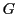 は次を満たしているとする.
は次を満たしているとする.
- (1)
- ちょうど
 個の複素数からなる
個の複素数からなる 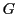 の例をあげよ.
の例をあげよ.
- (2)
- ちょうど
 個の複素数からなる
個の複素数からなる 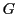 は (1) の例以外にないことを示せ.
は (1) の例以外にないことを示せ.
入試問題 31 (解答
31)
[95 京大文系後期]
自然数  の関数
の関数 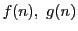 を
を
によって定める.
- (1)
- すべての自然数
 に対して
に対して 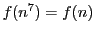 を示せ.
を示せ.
- (2)
- あなたの好きな自然数
 を一つ決めて
を一つ決めて 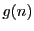 を求めよ.
その
を求めよ.
その 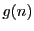 の値をこの設問(2)におけるあなたの得点とする.
の値をこの設問(2)におけるあなたの得点とする.


 次: 相互法則
上: 剰余類
前: 指数
Aozora Gakuen
次: 相互法則
上: 剰余類
前: 指数
Aozora Gakuen
![]() を十進法で表して
を十進法で表して
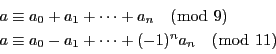
![]() であるとする.このとき
であるとする.このとき ![]() に対して
に対して
![]() を超えない自然数のうちで
を超えない自然数のうちで ![]() と互いに素であるものの
個数を
と互いに素であるものの
個数を
![]() とおく.
とおく.
![]() である.
である.
![]() で
で ![]() を超えない整数を表すと定理19,定理20の一般化として
を超えない整数を表すと定理19,定理20の一般化として
![\begin{eqnarray*}
\sum_{d\vert n}\varphi(d,\ dx)&=&[nx]\\
\varphi(n,\ x)&=&\sum_{d\vert n}\mu (d)\left[ \dfrac{x}{d} \right]
\end{eqnarray*}](images/img1221.gif)
![]() を用いよ.
を用いよ.
![]() 次の多項式
次の多項式
![]() を自然数とし,
を自然数とし,![]() を
を![]() より小さくかつ
より小さくかつ![]() と互いに素な自然数の総数とする.すなわち
と互いに素な自然数の総数とする.すなわち
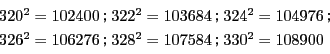
![]() を2以上の整数とする.2以上の整数
を2以上の整数とする.2以上の整数 ![]() に対し,次の条件(イ),(ロ)を
みたす複素数の組
に対し,次の条件(イ),(ロ)を
みたす複素数の組
![]() の個数を
の個数を ![]() とする.
とする.
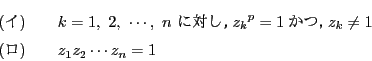
![]() は次を満たしているとする.
は次を満たしているとする.
![]() の関数
の関数 ![]() を
を