南海
定点
![]() をとおり,
ベクトル
をとおり,
ベクトル
![]() に直交する平面
に直交する平面 ![]() の方程式を求めよ.
の方程式を求めよ.
史織
平面上の任意の点
![]() をとる.
をとる.
二つのベクトル
![]() と
と
![]() が直交するので内積が0.
が直交するので内積が0.
![]() なので
なので
このベクトル
![]() のことを
平面
のことを
平面 ![]() の法線ベクトルという.
の法線ベクトルという.
南海
逆に一次式 ![]() を満たす点
を満たす点 ![]() はどんな図形になるかも同様にわかる.
はどんな図形になるかも同様にわかる.
つまりこの式を満たす任意の
![]() をとる.
をとる.
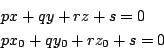
つまり二つのベクトル ![]() と
と
![]() が直交している.
したがって求める図形は点
が直交している.
したがって求める図形は点
![]() をとおり
をとおり![]() と直交する
平面になる.
と直交する
平面になる.