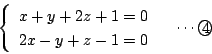
史織 では空間内の直線はどのように表されるのでしょうか.
南海 空間における直線は二つの平行でない平面の交わりによって定まる.だから 方程式としては,二つの一次式の連立で表される.
例えば
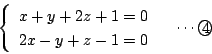
史織
点![]() をとおりベクトル
をとおりベクトル
![]() に平行な直線は
動点を
に平行な直線は
動点を ![]() とすれば
とすれば
南海 それを座標で書くとどうなるか.
史織
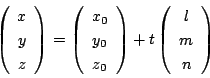
南海
この考え方でいくと![]() はどんな直線なのか.
はどんな直線なのか.
史織
二式を加えると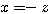 .これから
.これから 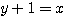 .これを
.これを ![]() の形に書くと
の形に書くと
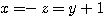
するとこれは定点 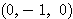 をとおりベクトル
をとおりベクトル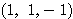 に平行な
直線なんだ.ベクトルを用いて書けば
に平行な
直線なんだ.ベクトルを用いて書けば
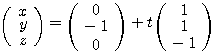
南海 練習問題を出しておこう.