となる整数
南海 まず整数論の入り口である,除法と,除法を用いた論証の復習だ.
この証明そのものは『数論初歩』を見てほしい. 重要なので概略を示す.
まず.整数 ![]() と正整数
と正整数![]() に対して
に対して
『数論初歩』ではさらに厳密に, 自然数の部分集合には最小の要素が存在することを根拠に証明した.
そこで ![]() とおく.
とおく.
![]() より
より![]() で
で
あとはこのような ![]() が二通りあったとして,相等しいことを示せばよかった.
が二通りあったとして,相等しいことを示せばよかった.
南海 どのように導かれるのか,確認しよう.
まず,整数![]() が
が![]() の倍数でるとは,
の倍数でるとは,![]() となる整数が存在することと定める.
となる整数が存在することと定める.
すると,割り算ができ,![]() を
を![]() で割った商と余りが一意に確定することによって,
で割った商と余りが一意に確定することによって,
が
の倍数であることは,
を
で割った余りが0であることと同値である.
太郎
そこで質問ですが,例えば6の約数は普通2や3ということになりますが,
![]() や
や![]() も約数ではないのですか.
も約数ではないのですか.
南海 その通りだ.
素数は正のもので考えるので![]() を素因数分解とはいわないのだが,
因数分解であることには変わりない.
を素因数分解とはいわないのだが,
因数分解であることには変わりない.
このように,約数や倍数,![]() の自由さがあり,
整除に関することは
の自由さがあり,
整除に関することは![]() の違いを除いて決まる.
これを前提にして,正の方で代表させて考えるのである.
の違いを除いて決まる.
これを前提にして,正の方で代表させて考えるのである.
太郎
![]() は特別な数なのですか.
は特別な数なのですか.
南海
そう.整数のなかで逆数もまた整数であるのは,![]() だけだ.
このような数を単数というのだが,普通の整数では単数は
だけだ.
このような数を単数というのだが,普通の整数では単数は![]() だけだ.
だけだ.
太郎 「普通の整数」でないものとは『数論初歩』に少し書かれていた二次体の整数とかですか.
南海 そうだ.いわゆる「代数的整数」だ. この話はここではこれ以上はできないが, 実二次体の整数では単数が無数にある.
普通,整数といっているものは有理整数という.
太郎
有理整数では単数は![]() だけなのですね.
そして,割り切れるとか,因数分解とか,
すべて,ある整数で成り立てば,
それに
だけなのですね.
そして,割り切れるとか,因数分解とか,
すべて,ある整数で成り立てば,
それに![]() をかけても,成り立つのですね.
をかけても,成り立つのですね.
南海 『数論初歩』でもそのことは書かれているが, 少しわかりにくかったかもしれない.
そこでいくつかの定義.
0およびでない整数
は少なくとも
と
を約数を持つ.
および
以外の約数を「真の約数」ともいう.
真の約数を持たない正の整数を 素数 という.
真の約数を持つ整数を 合成数 という.
さらに,公約数,公倍数が定義される.
太郎 『数論初歩』に次のように公倍数,公約数の定義があります.
二つ以上の整数に共通な倍数をそれらの整数の公倍数という. 0は常に公倍数である. それを除けば公倍数の絶対値は
のいずれの絶対値よりも小さくはないので, 公倍数の中に正で最小のものがある. それを最小公倍数(least common multiple 略して L.C.M.)という.
二つ以上の整数同様の理由で,公約数,公倍数は正のもので考えるのですね.に共通な約数をそれらの整数の公約数という. 1は常に公約数である. 公約数の絶対値は
のいずれの絶対値よりも大きくはないので, 公約数の中に最大のものがある. それを最大公約数(greatest common measure 略して G.C.M.)という.
南海 最大公約数が1であるとき,その2数は互いに素であるという.
そこで,次の定理の(1)を示してほしい. 他はこれをもとに示される. それは『数論初歩』にある.
太郎 はい.
証明
![]() の最小公倍数を
の最小公倍数を
![]() とし,
とし, ![]() を任意の公倍数とする.
を任意の公倍数とする.
![]() を
を ![]() で割った商を
で割った商を ![]() ,余りを
,余りを ![]() とすると
とすると
南海 この定理の証明において, 「除法の原理」が基本定理として用いられてることがわかる. 日頃当然のように論証で使っていることが, 「除法の原理」を基礎に厳密に示される.
南海
次に因数分解を考えよう.
先に見たように,因数分解は
整数![]() をこれ以上分解できないところまで分解して,
をこれ以上分解できないところまで分解して,
![]() は異なる素数,
は異なる素数,
![]() は正の整数である.
は正の整数である.
合成数は素数の積として順序を除けばただ一通りに表すことができる. これが素因数分解の一意性といわれる基本定理である.
南海
この証明は『数論初歩』をみてほしい.
概略をいえば,分解できることは数学的帰納法で示す.
一意性の証明は,整数の積![]() を素数
を素数![]() が割り切れば,
が割り切れば,
![]() は
は![]() または
または![]() を割り切る,ということを用いる.
これは先の定理2の(4)からわかる.
を割り切る,ということを用いる.
これは先の定理2の(4)からわかる.
太郎 なるほど.すべて除法が論証の根拠になっているのですね.
南海 最近,次のような除法を用いない因数分解の一意性の証明を『数学のたのしみ』 (2006年夏号,日本評論社)の「素数・ゼータ関数・三角関数」(黒川重信)で教えられた. ツェルメロによるものであるということだ.
それを紹介しよう. これは除法を用いていない. 自然数の集合には最小のものが存在することだけを用いている.
因数分解の可能性は同様なので,一意性のみ別証明をおこなう.
因数分解の一意性の別証明
異なる因数分解をもつ自然数の集合を考える.
この集合に属する最小の自然数を![]() とする.
とする.
![]() は相異なる2つの因数分解をもつ.それを
は相異なる2つの因数分解をもつ.それを
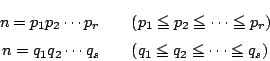
また,
![]() のいずれも
のいずれも
![]() のいずれとも異なる.
なぜなら,もし
のいずれとも異なる.
なぜなら,もし![]() なら,
これを約せば
なら,
これを約せば![]() より小さい数で,異なる因数分解をもつ自然数が得られ,
より小さい数で,異なる因数分解をもつ自然数が得られ,
![]() がそのような数のなかで最小であることに反する.
がそのような数のなかで最小であることに反する.
![]() とする.
ここで自然数
とする.
ここで自然数![]() を
を
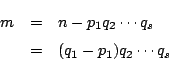
この![]() の因数分解における因数
の因数分解における因数![]() は
は![]() の倍数ではない.
なぜならもし
の倍数ではない.
なぜならもし![]() の倍数なら
の倍数なら![]() が
が![]() の倍数となり互いに異なる素数であることに反する.
よってこの因数分解に
の倍数となり互いに異なる素数であることに反する.
よってこの因数分解に![]() は現れない.
は現れない.
一方![]() は
は
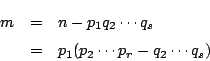
よって![]() の2つの因数分解は相異なる因数分解である.
の2つの因数分解は相異なる因数分解である.
![]() なので,
なので,
![]() が異なる2つの因数分解をもつ最小の自然数であることと矛盾した.
が異なる2つの因数分解をもつ最小の自然数であることと矛盾した.
したがって異なる2つの因数分解をもつ自然数は存在しない.□
太郎 わかりました.
除法の原理自身,除法が一意に出来ることを示すためには 自然数の集合には最小のものが存在することを用いるのでした.
だから,除法を使うか使わないかにかかわらず,自然数の性質が土台になっています.
南海 そうなのだ. だから,このツェルメロの証明は, 自然数の集合には最小のものが存在することをいったん除法の原理にまとめることをせず, 自然数の性質から直接示す,ともいえる.
これを参考にして, 後で整式の因数分解の一意性の証明もおこないたい.
南海 もう一つ,証明に除法が使われる基本定理を紹介しよう.
証明
条件から![]() である.
その結果,
である.
その結果,![]() なら
なら
![]() である.
である.
また,自然数![]() に対して
に対して![]() のとき
のとき
そこで![]() の要素のうち,正の要素からなる部分集合に属する最小の要素を
の要素のうち,正の要素からなる部分集合に属する最小の要素を![]() とする.
自然数の集合には最小の要素が存在するので,
とする.
自然数の集合には最小の要素が存在するので,![]() はつねに存在する.
はつねに存在する.
![]() の任意の要素
の任意の要素![]() をとり,それを
をとり,それを![]() で割る.
で割る.
ここでもし![]() なら
なら![]() が正で最小の要素であることに反する.
よって
が正で最小の要素であることに反する.
よって![]() ,つまり
,つまり![]() の任意の要素
の任意の要素![]() は
は![]() の倍数である.
の倍数である.
逆に,![]() の倍数が
の倍数が![]() に属することはすでに示した.
に属することはすでに示した.
したがって
![]() が示せた.□
が示せた.□
南海
この![]() ように,
差と整数倍が再び
ように,
差と整数倍が再び![]() に属するような部分集合をイデアルというのだが,
有理整数のイデアルは,ある整数の倍数全体になる,ことを意味している.
に属するような部分集合をイデアルというのだが,
有理整数のイデアルは,ある整数の倍数全体になる,ことを意味している.
南海 これを用いると次のことが示される.
太郎 この事実は知っていますが,証明は部屋割り論法を用いるものです.
部屋割り論法による証明
南海 まづそれを復習しよう. 次の演習問題を解いてみてほしい.
太郎 (1) 対偶を示す.
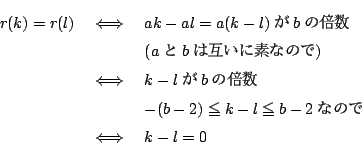
(2)
![]() と
と ![]() が互いに素なので,
が互いに素なので,
![]() に対して
に対して ![]() は
は![]() の倍数とはならない.
ゆえにこのとき
の倍数とはならない.
ゆえにこのとき
![]() である.
である.
一方 ![]() ならば
ならば ![]() なので
なので
![]() はすべて異なる
はすべて異なる ![]() 個の整数で,
すべて
個の整数で,
すべて
![]() をみたす.
をみたす.
ゆえに鳩の巣原理により
![]() は
は
![]() の各値を一つずつとる.
ゆえに
の各値を一つずつとる.
ゆえに![]() となる
となる
![]() が存在する.
つまり
が存在する.
つまり![]() が
が ![]() の倍数である.これを
の倍数である.これを ![]() とおくと
とおくと
南海 この演習問題も,入試問題の改題だが, 高校数学ではこのように(1)を用いていわゆる部屋割り論法で 証明するのが普通だ.
実は定理4を用いる次の証明法の方が一般的だ.
なぜなら,変数を増やして![]() の最大公約数が1なら
の最大公約数が1なら
![]() ,
,![]() が
が![]() に属せば
に属せば
したがって定理4より
![]() は,
は,![]() に属するある整数
に属するある整数![]() の倍数の全体である.
の倍数の全体である.
![]() とする.
とする.
一方