南海 以上の議論を,整式の場合に行おう,というのが今日の主題だ.
ここで,整式の整数論がどのように成りたつかを考えていくのだが, 少し準備的な考察が必要だ.
それは係数をどこにとるかだ.
太郎 有理数係数とか,実数係数とかですか.
南海
普通は実数を係数とする整式全体を考える.
このような実数係数の整式の集合を,変数を明示して
![]() と表そう.
と表そう.
以下のことは
![]() で考えても,有理数係数にかぎって
で考えても,有理数係数にかぎって![]() で考えても,
また複素数で考え
で考えても,
また複素数で考え![]() としても同じことである.
そこで,
としても同じことである.
そこで,![]() を有理数の集合
を有理数の集合![]() ,
実数の集合
,
実数の集合![]() ,複素数の集合
,複素数の集合![]() のいずれかを表すものとし,
これからは
のいずれかを表すものとし,
これからは![]() に係数をもつ整式の集合
に係数をもつ整式の集合![]() を考えることにしよう.
を考えることにしよう.
ただし, 整数係数で考えるときはまた別であることには注意したい.
![]() の整式は,つぎの除法の基本性質をもつ.
ここで
の整式は,つぎの除法の基本性質をもつ.
ここで![]() は整式
は整式 ![]() の次数を表す.
の次数を表す.
証明
![]() ならば
ならば
![]() でよい.
でよい.
![]() のとき,
のとき,
![]() とする.
とする. ![]() と
と ![]() の
の ![]() 次の項をそれぞれ
次の項をそれぞれ
![]() とする.
とする.
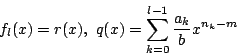
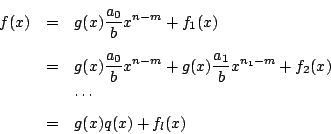
これが1組しかないことを示す.2組あったとする.
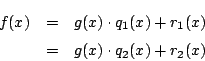
ところが一方,
![]() だから,
だから,
![]() .これは矛盾.
.これは矛盾.
ゆえに等式(1)が成立するのは,
![]() のときのみである.
このとき,
のときのみである.
このとき,
![]() となる.□
となる.□
南海
まず,整数の場合と同じように,
整式![]() が整式
が整式![]() の倍数であるとは,
の倍数であるとは,
![]() を満たす整式
を満たす整式![]() が存在することと定義する.
が存在することと定義する.
整式の場合も割り算ができ,
![]() を
を![]() に対して,
に対して,![]() を
を![]() で割った商と余りが一意に確定することから,
で割った商と余りが一意に確定することから,
が
の倍数であることは,
を
で割った余りが0であることと同値である.
太郎
因数分解は
南海 その通りだ.
このように,約数や倍数,因数分解は,定数倍の違いを除いて決まる.
太郎
![]() の中で,0でない定数は逆数もまた整式です.
逆数もまた整式となるのは0でない定数にかぎります.
の中で,0でない定数は逆数もまた整式です.
逆数もまた整式となるのは0でない定数にかぎります.
![]() では0でない定数が単数なのですね.
では0でない定数が単数なのですね.
南海
0および定数でない整式は少なくとも定数と
を約数を持つ. これら以外の約数を真の約数という. 真の約数を持たない整式を 既約 という.
既約かどうかは,定数倍しても変わらない.
既約な整式というのは,整数での素数と同じ役割を果たす.
ここで注意.
既約かどうかは,係数をどこで考えるかによって異なる. 例を挙げてほしい.
太郎
![]() は
は
南海 そう.だから既約かどうかは係数をどこにとるかで変わり, 整式固有の性質ではない.
太郎 だからあまり素数とはいわないのですね.
南海
さらに整数のときと同様に,公約数,公倍数が定義される.
整数では![]() 倍を除いて考えるところを,
整式では0でない定数倍を除いて考えることにすれば,まったく同じである.
倍を除いて考えるところを,
整式では0でない定数倍を除いて考えることにすれば,まったく同じである.
公約数や公倍数は整数の場合と同じである.
2つの整式![]() と
と![]() がある.
がある.
最大公約数とは,![]() と
と![]() の公約数のなかで,
次数が最も大きいものをいう.
最大公約数が定数のとき,
の公約数のなかで,
次数が最も大きいものをいう.
最大公約数が定数のとき,
![]() と
と![]() は互いに素であるという.
は互いに素であるという.
最小公倍数とは,![]() と
と![]() の公倍数のなかで,
次数が最も小さいものをいう.
の公倍数のなかで,
次数が最も小さいものをいう.
太郎 最大公約数も最小公倍数も定数倍を除いて一つに定まる.
南海
それは証明が必要だ.
それを含めて次の定理の証明を整数の場合にならって構成してほしい.
簡単のために,![]() や
や![]() などで整式を表すことにする.
すると整数の場合の証明が,ほんの一部の手直しでそのまま使える.
どこを直せばよいか考えてみてほしい.
などで整式を表すことにする.
すると整数の場合の証明が,ほんの一部の手直しでそのまま使える.
どこを直せばよいか考えてみてほしい.
南海 (1)を示してほしい.他はそれをもとに『数論初歩』と同様に示される.
太郎 整数の場合を手直しするところは, 絶対値を次数で考えるところです.
証明
![]() の最小公倍数を
の最小公倍数を
![]() とし,
とし, ![]() を任意の公倍数とする.
を任意の公倍数とする.
![]() を
を ![]() で割った商を
で割った商を ![]() ,余りを
,余りを ![]() とすると
とすると
南海 この定理の証明においても, 「除法の原理」が基本定理として用いられてることがわかる.
南海
さて,整式![]() を既約な整式の積に分解して,
を既約な整式の積に分解して,
![]() は異なる既約な整式,
は異なる既約な整式,
![]() は正の整数である.
は正の整数である.
このとき整数と同様に次の定理が成り立つ.
整式の場合も素因数分解の一意性という. 基本的な定理である.
太郎 この証明は整数の場合と同じですね. ここでも,除法が論証の根拠になっているのですね.
南海 そこでだ.整数の因数分解の一意性の証明にならって, 整式の場合についても,除法を用いないツェルメロの方法による別証明をしてみよう.
因数分解の一意性の別証明
異なる因数分解をもつ整式の集合を考える.
この集合に属する次数が最小の整式を![]() とする.
とする.
![]() は相異なる2つの因数分解をもつ.それを
は相異なる2つの因数分解をもつ.それを
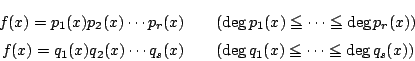
また,
![]() のいずれも
のいずれも
![]() のいずれとも異なる.
なぜなら,もし
のいずれとも異なる.
なぜなら,もし![]() なら,
これを約せば
なら,
これを約せば![]() より小さい次数で,異なる因数分解をもつ整式が得られ,
より小さい次数で,異なる因数分解をもつ整式が得られ,
![]() がそのような整式のなかで次数最小であることに反する.
がそのような整式のなかで次数最小であることに反する.
![]() とする.
とする.
![]() とすると,
適当な定数
とすると,
適当な定数![]() を
を
ここで整式![]() を
を
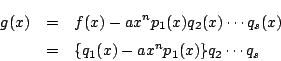
この![]() の因数分解における因数
の因数分解における因数
![]() は
は![]() の倍数ではない.
なぜならもし
の倍数ではない.
なぜならもし![]() の倍数なら
の倍数なら![]() が
が![]() の倍数となり,
互いに異なる既約な整式であることに反する.
よってこの因数分解に
の倍数となり,
互いに異なる既約な整式であることに反する.
よってこの因数分解に![]() は現れない.
は現れない.
一方![]() は
は
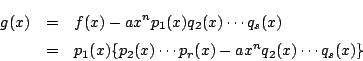
よって![]() の2つの因数分解は相異なる因数分解である.
の2つの因数分解は相異なる因数分解である.
![]() なので,
なので,
![]() が異なる2つの因数分解をもつ次数最小の整式であることと矛盾した.
が異なる2つの因数分解をもつ次数最小の整式であることと矛盾した.
したがって異なる2つの因数分解をもつ整式は存在しない.□
南海 もう一つ,整数の場合と同様に, 証明に除法が使われる基本定理を紹介しよう.
南海 これが,整式のイデアルの定義だ. 整式のイデアルはある整式の倍数全体になる,ということだ.
太郎
証明
条件から
![]() である.
その結果,
である.
その結果,![]() なら
なら
![]() である.
である.
そこで![]() の要素のうち,
次数最小の整式
の要素のうち,
次数最小の整式![]() をとる.
をとる.
![]() の任意の要素
の任意の要素![]() をとり,それを
をとり,それを![]() で割る.
で割る.
ここでもし![]() なら
なら![]() が次数最小の要素であることに反する.
よって
が次数最小の要素であることに反する.
よって![]() ,つまり
,つまり![]() の任意の要素
の任意の要素![]() は
は![]() の倍数である.
の倍数である.
したがって
![]() が示せた.□
が示せた.□
南海 これを用いると次のことが示される.
太郎 整式の場合,余りが有限個ではないので部屋割り論法を用いる 方法はうまくいかないようです.
太郎
![]() ,
,
![]() が
が
![]() に属せば
に属せば
したがって定理9より
![]() は,
は,![]() に属するある整式
に属するある整式![]() の倍数の全体である.
の倍数の全体である.
![]() とする.
とする.
一方
つまり
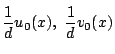 は
は
太郎 ユークリッドの互除法も同じようにできるのですか.
南海
簡単のために整式![]() の最大公約数を
の最大公約数を ![]() と書く.
演習問題にしたものあがるのでやってみてほしい.
と書く.
演習問題にしたものあがるのでやってみてほしい.
太郎 解いてみます.
(1)
![]() ,
,
![]() とします.
とします.
![]() ,
,
![]() .また
.また
![]() ,
,
![]() とします.
とします.
一方
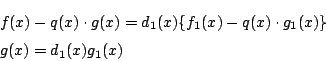
つまり![]() が示された.
が示された.
(2)
![]() を
を ![]() で割った商を
で割った商を![]() とすると,余りが
とすると,余りが![]() なので
なので
(3)