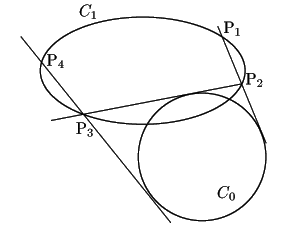
次のようなときにもポンスレの閉形定理を考えることができるのではないか.
拓生
![]() 上の
点
上の
点![]() から
から![]() に接線を引き,
接線上にある
に接線を引き,
接線上にある![]() の上のもう一つの点を
の上のもう一つの点を![]() とする.
点
とする.
点![]() から
から![]() に接線を引き,
接線上にある
に接線を引き,
接線上にある![]() の上のもう一つの点を
の上のもう一つの点を![]() とする.
点
とする.
点![]() から
から![]() に接線を引き,
接線上にある
に接線を引き,
接線上にある![]() の上のもう一つの点を
の上のもう一つの点を![]() とする.….
とする.….
これを繰りかえして,元の![]() に戻ってくるかということですね.
に戻ってくるかということですね.
ある点![]() からはじめて
からはじめて![]() 回で元に戻れば,どこからはじめても元に戻るか.
確かにこのように考えれば,位置関係は自由です.
回で元に戻れば,どこからはじめても元に戻るか.
確かにこのように考えれば,位置関係は自由です.
拓生 4本,3本,2本,なし,のいろいろあるように思われます.
まず先に考えた円と円で![]() の場合の例をもう一度考えよう.
の場合の例をもう一度考えよう.
![\begin{eqnarray*}
H(t)&=&<(r-a)\{(r+a)^2-t^2-1\}+(r+a)[\{(r-a)^2-1\}t^2-1]>^2\\
&&-\{(r+a)^2+(r-a)^2t^2\}^2
\end{eqnarray*}](images/img158.gif)
![]() 上の点
上の点
![]() が
が
拓生
接線の式は
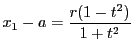 を代入する.
を代入する.
なぜ![]() のとき,
のとき,![]() は共通接線を与える式になるのか.
でもそれが虚根ということは?
は共通接線を与える式になるのか.
でもそれが虚根ということは?
南海
拓生
共通接線を![]() とおきます.両方と接するので
とおきます.両方と接するので
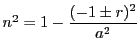 ,
だから接線は
,
だから接線は
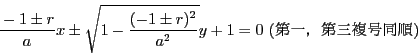
南海
図形的にはともかく,それぞれの円の式と連立させて共通根を求めれば,それが重根になることはまちがいない.もちろん点と直線の距離の式は使えないが,![]() か
か![]() を消去して得られる二次式の判別式をとれば,距離の式から得られる式と同じ式が得られる.つまり虚根も考えれば,上の接線の式は
を消去して得られる二次式の判別式をとれば,距離の式から得られる式と同じ式が得られる.つまり虚根も考えれば,上の接線の式は![]() の双方と重根をもつ.そういう意味ではもとの二つの二次曲線とそれぞれ重根をもつ共通接線はつねに4本あるということになる.
の双方と重根をもつ.そういう意味ではもとの二つの二次曲線とそれぞれ重根をもつ共通接線はつねに4本あるということになる.
拓生
![]() なら
なら![]() の解は一つ.
の解は一つ.
![]() の解が二つになるのは,
の解が二つになるのは,
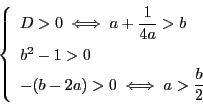
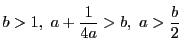 のときで,
位置関係はそれぞれ図のようになり,共通接線はそれぞれ2本,4本,4本である.
のときで,
位置関係はそれぞれ図のようになり,共通接線はそれぞれ2本,4本,4本である.
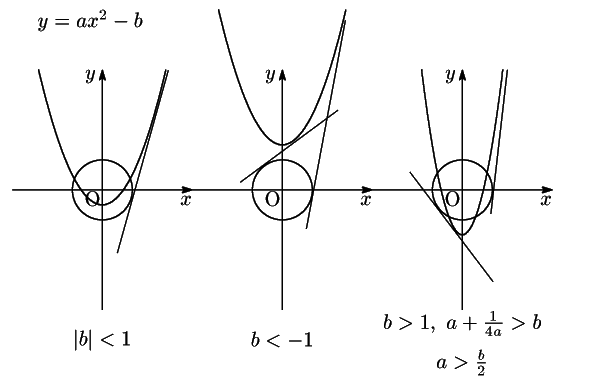
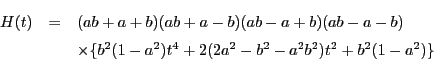
南海
![]() の場合をまとめる.
の場合をまとめる.
![]() を円
を円![]() とし,
とし,![]() を次のようにとる.
このときの
を次のようにとる.
このときの![]() ,
,![]() である.
である.
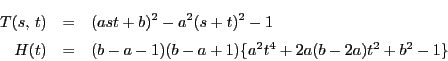
![\begin{eqnarray*}
T(s,\,t)&=&\{(r-a)st+r+a\}^2-(st-1)^2-(s+t)^2\\
H(t)&=&\{(r^2-a^2)^2-4r^2\}[\{(r-a)t^2+r+a\}^2-(t^2+1)^2]
\end{eqnarray*}](images/img372.gif)
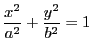 .
.
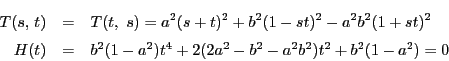
このように以上の例は,![]() のときは,
のときは,
![]() から共通接線が引けるような
から共通接線が引けるような![]() が,
が,
![]() を頂点とする三角形が出来る条件式を満たす
ことを示している.
を頂点とする三角形が出来る条件式を満たす
ことを示している.
これはなぜだろうか.
![]() のときの
のときの![]() の構成法にかなった方程式
の構成法にかなった方程式![]() の自明な
解が,共通接線となる4個の
の自明な
解が,共通接線となる4個の![]() なのだ.
なのだ.
![]() をどのように構成したか.図の上のように,
をどのように構成したか.図の上のように,
![]() から2本の接線
から2本の接線
![]() ,
,
![]() を引く.直線
を引く.直線
![]() が
が![]() に接する条件が
に接する条件が![]() であった.
であった.
点![]() を共通接線になる点とする.このときは
を共通接線になる点とする.このときは
![]() となる.よって作り方から直線
となる.よって作り方から直線
![]() は
は![]() に接する.
に接する.
かくして4次方程式![]() はつねに4個の自明な根をもつ.
したがってその他にもう1個これを満たす根があれば
はつねに4個の自明な根をもつ.
したがってその他にもう1個これを満たす根があれば![]() は恒等式となり
すべての
は恒等式となり
すべての![]() で成立する.
で成立する.
拓生
これは![]() の場合の一般的な証明になっています.
の場合の一般的な証明になっています.
すでに計算を行った楕円と円で![]() のときと同様に,
放物線と円で
のときと同様に,
放物線と円で![]() のときを計算してみる.
実際の計算はRisa/Asirで行った.
のときを計算してみる.
実際の計算はRisa/Asirで行った.

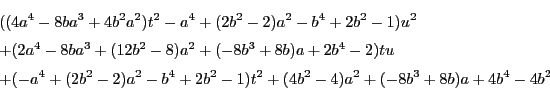
南海 この場合も,式の図形的な意味はよくわからない.
拓生
円と二次曲線のいくつかの実例では,
すべて最後に点![]() を媒介変数表示したときの変数
を媒介変数表示したときの変数![]() についての4次方程式が得られました.そしてそれが恒等的に0になることを示そうとしました.
恒等的に0になるためには,実根でなくても虚根を含めて,
しかも重根の場合は重複度も含めて,次数より1多い根があればそれで恒等的に0になるのでした.図形から出発したので実数解ばかり考えますが,恒等式かどうかの判断は実数でなくてもよい.
についての4次方程式が得られました.そしてそれが恒等的に0になることを示そうとしました.
恒等的に0になるためには,実根でなくても虚根を含めて,
しかも重根の場合は重複度も含めて,次数より1多い根があればそれで恒等的に0になるのでした.図形から出発したので実数解ばかり考えますが,恒等式かどうかの判断は実数でなくてもよい.
![]() のときは自明な4解があり,その他に1解があれば恒等式なることがわかりました.これは,共通接線が実座標平面上にあってもなくても,かまいませんでした.
のときは自明な4解があり,その他に1解があれば恒等式なることがわかりました.これは,共通接線が実座標平面上にあってもなくても,かまいませんでした.
![]() のとき入試問題では
のとき入試問題では![]() が虚数解をもち,かつ座標平面上に一つの四角形が存在することから,恒等式であることを示しました.
が虚数解をもち,かつ座標平面上に一つの四角形が存在することから,恒等式であることを示しました.
しかし![]() のとき,自明な4解の存在はまだ見いだせていません.
一般的にはつねに虚数解とはかぎらないので,
この段階ではつねに恒等式なるとはまだいえていません.
のとき,自明な4解の存在はまだ見いだせていません.
一般的にはつねに虚数解とはかぎらないので,
この段階ではつねに恒等式なるとはまだいえていません.
そのため
媒介変数![]() と曲線の置かれた場である平面も,すべて射影空間で考えなければならない.
また,すべて複素数体上で考えなければならない.
と曲線の置かれた場である平面も,すべて射影空間で考えなければならない.
また,すべて複素数体上で考えなければならない.
拓生
媒介変数を射影直線にすることで,
例えば楕円の場合に![]() を除くという例外がなくなる.
また,二次曲線を射影平面で考えることで,放物線と円の場合にあった,
「
を除くという例外がなくなる.
また,二次曲線を射影平面で考えることで,放物線と円の場合にあった,
「![]() 座標が
座標が![]() と異なる
と異なる![]() 上の点」という例外がいらなくなる.
上の点」という例外がいらなくなる.
南海 そうだ.そこで話を進めよう.
射影直線![]() を次のように定める.
を次のように定める.
![]() でない複素数の組
でない複素数の組![]() の集合を考える.
の集合を考える.
![]() となる複素数
となる複素数![]() が存在するとき,
この二つの組は同値とし,
この同値関係で複素数の組
が存在するとき,
この二つの組は同値とし,
この同値関係で複素数の組![]() の集合を類別したものを,
一次元射影空間といい
の集合を類別したものを,
一次元射影空間といい![]() と表す.
これは実軸に無限遠点を加えたものを複素数に拡張したものである.
と表す.
これは実軸に無限遠点を加えたものを複素数に拡張したものである.
同様に
射影平面![]() を次のように定める.
を次のように定める.
![]() でない複素数の組
でない複素数の組
![]() の集合を考え,
の集合を考え,
![]() となる複素数
となる複素数![]() が存在するとき,
この二つの組は同値とする.
この同値関係で複素数の組
が存在するとき,
この二つの組は同値とする.
この同値関係で複素数の組
![]() の集合を類別したものを,
二次元射影空間といい
の集合を類別したものを,
二次元射影空間といい![]() と表す.
今後
と表す.
今後
![]() を必要に応じて
を必要に応じて![]() のような大文字で表そう.
のような大文字で表そう.
拓生
二次曲線![]() を射影座標で表す.
を射影座標で表す.
南海
そう.これをそのまま係数を複素数まで認めることにして拡張すればよい.
ちなみに行列
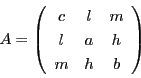
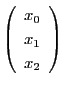 を表す.
を表す.
『射影幾何』では標準的なベクトルを縦ベクトルことが多いが,いずれでもよい.
さて複素数体上の二次曲線
![]() は適当な一次変換によって
は適当な一次変換によって
つまり二次曲線![]() 上の点
上の点![]() は2次の同次式を用いて
は2次の同次式を用いて
次に二次行列
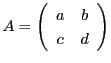 に対して
に対して![]() を行列式といい
を行列式といい
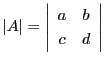 と表す.
さらに三次行列
と表す.
さらに三次行列
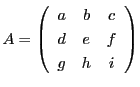 に対しその行列式
に対しその行列式![]() を
を
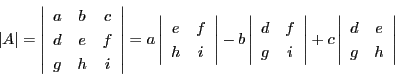
二つの二次曲線![]() と
と![]() がある.
がある.![]() 上の2点
上の2点
![]() が
それぞれ媒介変数
が
それぞれ媒介変数
![]() で表されているとする.
直線
で表されているとする.
直線![]() が
が![]() に接するための必要十分条件は,
に接するための必要十分条件は,
![]() のそれぞれに関する二次の等式で表される.
のそれぞれに関する二次の等式で表される.
証明
二次曲線![]() と
と![]() はそれぞれ行列
はそれぞれ行列![]() と
と![]() をもちいて
をもちいて
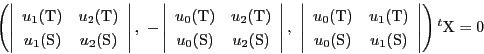
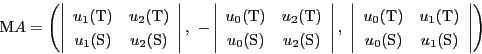
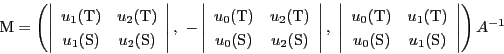
この![]() を
を![]() の方程式
の方程式
![]() に代入すると,
確かに
に代入すると,
確かに
![]() のそれぞれに関する二次の等式になっている.□
のそれぞれに関する二次の等式になっている.□
この双二次式を
![]() と表す.
またこの式を
と表す.
またこの式を
![]() とも表す.
とも表す.
二つの二次曲線![]() と
と![]() がある.
がある.
![]() 上の点
上の点![]() から
から![]() にひとつの接線をひき,
その延長が再び
にひとつの接線をひき,
その延長が再び![]() と交わる点を
と交わる点を![]() とする.
とする.
![]() から
から![]() に
に
![]() とは異なる接線をひき,
その延長が再び
とは異なる接線をひき,
その延長が再び![]() と交わる点を
と交わる点を![]() とする.
このようにして点
とする.
このようにして点![]() を定める.
を定める.
点![]() が媒介変数
が媒介変数![]() で表され,
点
で表され,
点![]() が媒介変数
が媒介変数![]() で表されるとすると
で表されるとすると
![]() と
と![]() の間には,それぞれについて二次の関係式
の間には,それぞれについて二次の関係式
証明
数学的帰納法で示す.
![]() のとき.
のとき.
![]() なので成立する.
なので成立する.
![]() のとき.
のとき.
![]() として,連立方程式
として,連立方程式
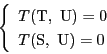
![]() は2個とれて,その各々から
は2個とれて,その各々から![]() には
には
![]() ともう一つの接線が引ける.
よってこの関係式は
ともう一つの接線が引ける.
よってこの関係式は
![]() を重根にもつ.その二次関係式で約分される.
その式を
を重根にもつ.その二次関係式で約分される.
その式を
![]() とすれば.
とすれば.
![]() は
は![]() と
と![]() のそれぞれに関して二次式で,
のそれぞれに関して二次式で,
![]() の2根が
の2根が![]() を与える.
を与える.
![]() に対して
に対して
![]() が定まったとする.
連立方程式
が定まったとする.
連立方程式
![]() ,
,![]() のとき.
のとき.
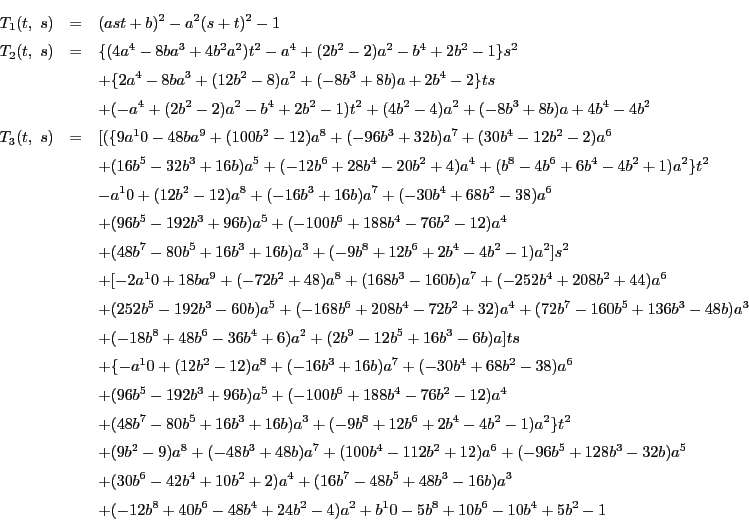
拓生
この結果,![]() とおいた式から4次方程式が得られる.
とおいた式から4次方程式が得られる.
![]() のときは,これまでの方法で
のときは,これまでの方法で![]() を作ると,共通接線から4個の自明な解があり,
その他に一つあれば恒等式でした.
を作ると,共通接線から4個の自明な解があり,
その他に一つあれば恒等式でした.
![]() のときはまだ一般的には解けていません.
のときはまだ一般的には解けていません.
南海
以下では簡単のために媒介変数を非斉次でとり,小文字の![]() などを使おう.
などを使おう.
![]() のとき.
のとき.
![]() 個の点を
個の点を
拓生
あっ,そうか.![]() ならこの時点で恒等式とわかるのだ.
ならこの時点で恒等式とわかるのだ.
![]() のときだけが残った.
のときだけが残った.
南海
実はこの場合もできるのだ.
![]() の
の![]() 個の解として
個の解として
![]() が存在したが,
これらは重根のはずだ.
が存在したが,
これらは重根のはずだ.
一般に![]() を固定すると
を固定すると
拓生
ということは![]() に対して4次方程式
に対して4次方程式![]() は重複度も含めて
は重複度も含めて![]() 個の
根があるのか.
個の
根があるのか.
南海 これを定理にまとめておこう.
二つの二次曲線![]() と
と![]() がある.
がある.![]() とし,
とし,
![]() 上の点
上の点![]() から
から![]() にひとつの接線をひき,
その延長が再び
にひとつの接線をひき,
その延長が再び![]() と交わる点を
と交わる点を![]() とする.
とする.
![]() から
から![]() に
に
![]() とは異なる接線をひき,
その延長が再び
とは異なる接線をひき,
その延長が再び![]() と交わる点を
と交わる点を![]() とする.
このようにして点
とする.
このようにして点![]() を定める.
を定める.
![]() 上の点
上の点![]() で
で
![]() となるものが存在すれば,
任意の
となるものが存在すれば,
任意の![]() について
について
![]() となる.
■
となる.
■
証明
![]() に対し
点
に対し
点![]() が媒介変数
が媒介変数![]() で表されるとする.
で表されるとする.
一般に![]() と
と![]() の間には,それぞれについて2次の関係式
の間には,それぞれについて2次の関係式
さらに,
![]() を1から
を1から![]() のいずれかとして
のいずれかとして![]() とする.
とする.
![]() に対して4次方程式
に対して4次方程式![]() は重複度も含めて
は重複度も含めて![]() 個の
根をもつ.よって等式
個の
根をもつ.よって等式![]() は恒等式であり,
任意の
は恒等式であり,
任意の![]() に対して成立する.
に対して成立する.
![]() を任意にとり,順次
を任意にとり,順次![]() を定めるとき,
を定めるとき,
![]() となる.
□
となる.
□
南海
入試問題からはじめて,まずそれを完全な形で解いた.
すると,虚数解をもつ4方程式が現れる.
その正体を調べると,虚な共通接線を与える![]() の方程式だった.
こうして複素数の世界を垣間見た.
それをもとに図形的考察から離れて複二次式の代数的考察にうつり,
ポンスレの定理を証明した.
の方程式だった.
こうして複素数の世界を垣間見た.
それをもとに図形的考察から離れて複二次式の代数的考察にうつり,
ポンスレの定理を証明した.
入試問題を解明しようとし,そこに現れた式の意味を考えることで複素数の世界に至った. 高校数学や入試数学も学問として研究すれば, 代数幾何学の入り口に来る,ということだ.
しかしまだ手をつけていないところがある.
![]() 上の点
上の点![]() から
から![]() に接線を引く.
その接点を
に接線を引く.
その接点を![]() とする.
これらの点の媒介変数表示
とする.
これらの点の媒介変数表示
![]() と
と![]() に対し,
に対し,
![]() と
と![]() の間にどのような関係があるかということである.
ここから楕円曲線が現れる.
ここから先は『パスカルの定理と幾何学の精神』のなかの「ポンスレの定理」に譲ろう.
の間にどのような関係があるかということである.
ここから楕円曲線が現れる.
ここから先は『パスカルの定理と幾何学の精神』のなかの「ポンスレの定理」に譲ろう.