証明
この四面体を![]() とし,記号は同様に定める.
とし,記号は同様に定める.
四面体の体積を![]() とする.
面
とする.
面![]() と辺
と辺![]() のなす角の正弦と,
ベクトル
のなす角の正弦と,
ベクトル
![]() と辺
と辺![]() のなす角の余弦とは
絶対値が等しい.
したがって
のなす角の余弦とは
絶対値が等しい.
したがって
![\begin{eqnarray*}
V&=&\pm \dfrac{1}{3}\left(\dfrac{1}{2}\overrightarrow{a}\time...
...}[\overrightarrow{a},\ \overrightarrow{b},\ \overrightarrow{c}]
\end{eqnarray*}](images/img304.gif)
また四面体![]() の体積を
の体積を![]() とすると同様に
とすると同様に
![\begin{eqnarray*}
V'&=&\pm\dfrac{1}{6}\left[\overrightarrow{\mathrm{KL}},\
\o...
...}[\overrightarrow{x},\ \overrightarrow{y},\ \overrightarrow{z}]
\end{eqnarray*}](images/img308.gif)
これから![]() が値を最大になるのは,
が値を最大になるのは,![]() の値が最大になるということである.
の値が最大になるということである.
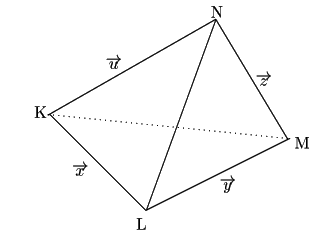
四面体![]() の4つの面の面積が与えられるということは,
四面体
の4つの面の面積が与えられるということは,
四面体![]() の4つの辺
の4つの辺
![]() の長さが与えられるということである.
の長さが与えられるということである.
そこで
![]() を固定し
を固定し
![]() を動かす.
を動かす.
![]() が最大になるのは2つの三角形が直交するときである.
つまり
が最大になるのは2つの三角形が直交するときである.
つまり![]() が最大になるときは,この2つの三角形に直交する2つのベクトル
が最大になるときは,この2つの三角形に直交する2つのベクトル
![]() と
と
![]() が直交している.
が直交している.