-
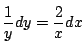 より
より
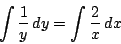
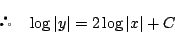
これから任意定数を置き直して
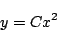
-
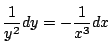 より
より
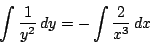
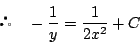
これから任意定数を置き直して
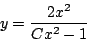
-
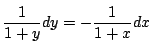 より
より
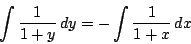
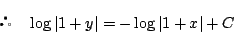
これから任意定数を置き直して
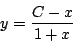
-
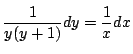 より
より
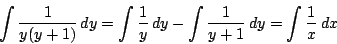
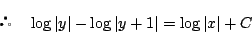
これから任意定数を置き直して
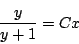
逆にとき任意定数を置き直して
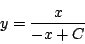
-
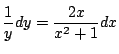 より
より
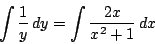
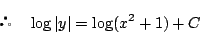
これから任意定数を置き直して
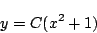
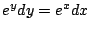 より
より
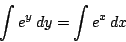
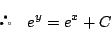
これから
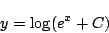
-
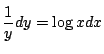 より
より
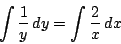
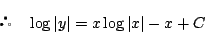
これから任意定数を置き直して
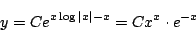
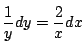 より
より
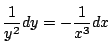 より
より
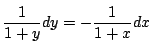 より
より
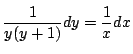 より
より
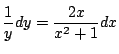 より
より
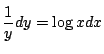 より
より
![]() のとき,
のとき,
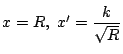 より
より
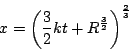
時刻![]() における水面の半径を
における水面の半径を![]() とする.
とする.
![]() なので
なので![]() とあわせて
とあわせて
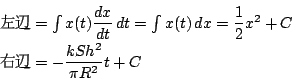
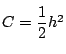
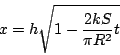
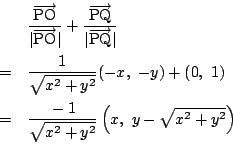
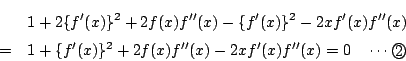
![]() から
から
![\begin{eqnarray*}
&&xf''(x)-x\{f'(x)\}^2f''(x)-f'(x)-\{f'(x)\}^3
+2x\{f'(x)\}^...
...\
&=&\left(xf''(x)-f'(x) \right)\left[1+\{f'(x)\}^2 \right]=0
\end{eqnarray*}](images/img289.png)
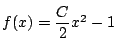 .
これを
.
これを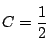 である.
である.
一方,この容器に単位時間あたり ![]() (一定)の割合で水を入れるので
(一定)の割合で水を入れるので
![]() から
から
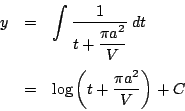
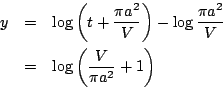
![]() を
を![]() に代入し,
に代入し,
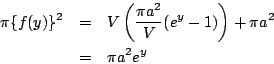
![]() なので
なので
さらに,![]() のとき
のとき![]() であるから
であるから
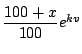 kg のガソリンを消費するので,
微分方程式
kg のガソリンを消費するので,
微分方程式
![]() のときの
のときの![]() の値
の値![]() が最初に積むガソリンの量である.
が最初に積むガソリンの量である.
一方,100km 離れたところに着く時刻は
![]() なので,
到着時のガソリンの残量は
なので,
到着時のガソリンの残量は
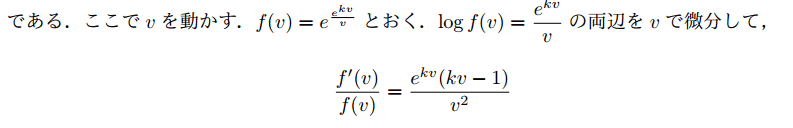
求める速度は![]() .ガソリンの量は
.ガソリンの量は![]() .
.