

 上: ζを関・ベルヌーイ数で表す
前: 係数定理
上: ζを関・ベルヌーイ数で表す
前: 係数定理
数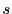 に対して
に対して
を「ゼータ関数」という.
実数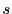 が
が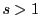 にあればこの級数は収束する.
にあればこの級数は収束する.
定理 2
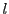
が与えられたとき,
ここに
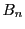
は関・ベルヌーイ数である.
■
証明
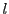 に対して自然数
に対して自然数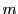 を十分大きくとる.
を十分大きくとる.
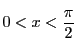 とする.このとき
とする.このとき
が成り立つ.各項は正なので
である.逆数をとって
となる.よって
である.ここに
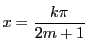 を代入し
を代入し
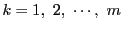 にわたって加える.
にわたって加える.
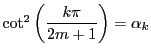 とおいたので
とおいたので
定理1によって
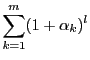 と
と
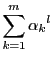 は
は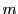 の多項式であり,いずれも
の多項式であり,いずれも
と表される.ただし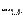 は次数
は次数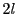 より低位の項を表す.
この結果,
より低位の項を表す.
この結果,
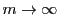 のとき,両辺は
のとき,両辺は
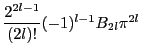 に収束する.つまり定理が示された.
□
に収束する.つまり定理が示された.
□
なお,
なので,
である.よって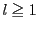 のとき
のとき
つまり,関・ベルヌーイ数は,第2項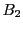 以降の偶数項は正負をくりかえすことも示された.
以降の偶数項は正負をくりかえすことも示された.
例 0.1.2
例
0.1.1を用いると次の値が得られる.
Aozora
2018-05-14
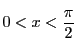 とする.このとき
とする.このとき
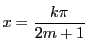 を代入し
を代入し
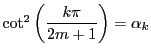 とおいたので
とおいたので
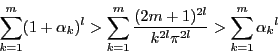
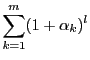 と
と
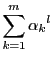 は
は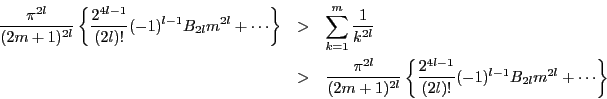
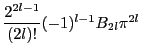 に収束する.つまり定理が示された.
□
に収束する.つまり定理が示された.
□