正の数 ![]() に対して
に対して ![]() とおくとき,次のことを示せ.
とおくとき,次のことを示せ.
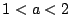 ならば
ならば 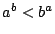 である.
である.
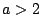 ならば
ならば 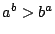 である.
である.
例題 2.8 [01日本女子大]
正の数 ![]() に対して
に対して ![]() とおくとき,次のことを示せ.
とおくとき,次のことを示せ.
考え方
この問題をどのように考えただろうか.
ノートに「 ![]() より…」と書いて,
それ以上に進めない人はいなかっただろうか.
(1)(2)の前提は「正の数
より…」と書いて,
それ以上に進めない人はいなかっただろうか.
(1)(2)の前提は「正の数 ![]() に対して
に対して ![]() 」だ.
この前提のもとに,(1)の論証の出発は確かに仮定「
」だ.
この前提のもとに,(1)の論証の出発は確かに仮定「![]() 」だ.
だから「
」だ.
だから「 ![]() より…」と書いて次を考えようとするのは理由のないことではない.
しかし,「
より…」と書いて次を考えようとするのは理由のないことではない.
しかし,「 ![]() より…」と書きはじめて,まっすぐに
結論「
より…」と書きはじめて,まっすぐに
結論「 ![]() 」に行き着くことは,簡単ではない.
」に行き着くことは,簡単ではない.

山の頂上を結論とし,麓を最初の仮定としよう.
麓からいくつか道が分かれているが,
山の途中には雲がかかっていて,
どの道を行けば頂上にたどり着けるかわからない,
これが問題に直面したときの状況だ.
ノートに「 ![]() より…」と書いてそこで次にすすめなかった人は,
このときに麓のどの道を行こうかわからず,あるいは道さえわからず,立ち止まってしまったようなものだ.
より…」と書いてそこで次にすすめなかった人は,
このときに麓のどの道を行こうかわからず,あるいは道さえわからず,立ち止まってしまったようなものだ.
こんなときはどうすればよいのだろう.
山登りを例にあげたが,実は山登りと問題を解くことには,重大な違いがある.
それは何か.山登りは麓から頂上へ向かって進むのだが,
問題を解くことは,
最初の仮定と最後の結論の間の道筋をつけることなのだ.
だから道は,頂上から麓へ降りていって発見しても良い.
この問題では結論![]() から逆にたどる.
から逆にたどる.
そこでこの問題をもう一度よく見ると,
「正の数 ![]() に対して」と書かれているが,
(1)は
に対して」と書かれているが,
(1)は![]() のとき,(2)は
のとき,(2)は![]() のとき,
結論の不等号が逆になっているので
結局,
のとき,
結論の不等号が逆になっているので
結局, ![]() の前提のもとで,
の前提のもとで,![]() か
か![]() かが
かが ![]() が2より大きいか小さいかで決まることを示せ,といっている.
これに注意して考えよう
が2より大きいか小さいかで決まることを示せ,といっている.
これに注意して考えよう
解答
![]() のとき
のとき
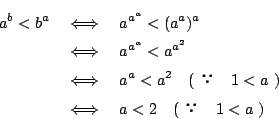
例題 2.9 [出典不明]
![]() のとき,次の不等式が成り立つことを証明せよ.
のとき,次の不等式が成り立つことを証明せよ.
考え方 結論を同値変形しよう.
解答
(1)
![]() より
より![]() なので
なので
(1)より
![]() なので,題意が示された.
なので,題意が示された.
(3)
![]() なので(1)より
なので(1)より