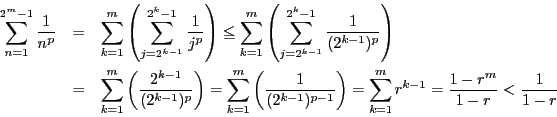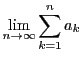 の略記とし,収束するときもしないときにも用いる.
この無限和を級数
の略記とし,収束するときもしないときにも用いる.
この無限和を級数
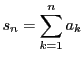 によって定まる数列
によって定まる数列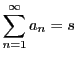 と表す.
収束しないとき,級数は発散するという.
級数が収束すれば
と表す.
収束しないとき,級数は発散するという.
級数が収束すれば
証明
級数
![]() の各項の絶対値を項とする級数
の各項の絶対値を項とする級数
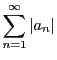 が収束するとき,
級数
が収束するとき,
級数
![]() は
絶対収束するという.
は
絶対収束するという.
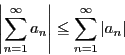
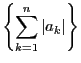 が基本数列なので,
任意の正数
が基本数列なので,
任意の正数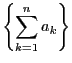 も基本数列となり,
も基本数列となり,
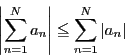
証明
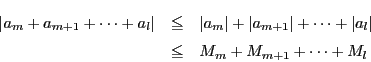
証明
証明 部分和
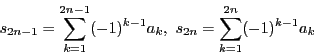
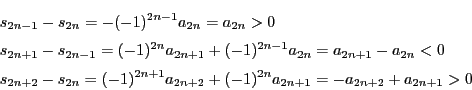
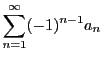 は収束する.
□
は収束する.
□
定理23のように符号が交互に変わる級数を交代級数という.
証明 一次結合に関する部分は
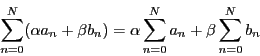
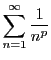 の収束性.
の収束性.
![]() のとき:発散する.
のとき:発散する.
この証明は定積分による評価
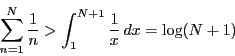
![]() のとき:発散する.
のとき:発散する.
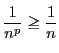 なので,
なので,
![]() のとき発散することから結論される.
のとき発散することから結論される.
![]() のとき:収束する.
のとき:収束する.
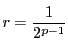 とおき,次のような級数の部分和をとる.
とおき,次のような級数の部分和をとる.
![]() である.
である.