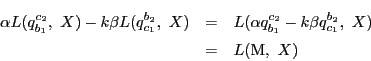次: 交点論による証明
上: パスカルの定理
前: 座標三角形による証明
次: 交点論による証明
上: パスカルの定理
前: 座標三角形による証明
19世紀になって代数的証明が見出された.その証明を,これまでの公理的射影幾何で確定した命題のもとに再構成する.
ここでは係数体は可換でかつ閉体であるとする.
補題 17
射影平面

上に,任意の5点を与えるとき,
これらすべてを通る二次曲線

が存在する.
これらの5点のうち,少なくとも4点が1直線上にないかぎり,

はただ一つに定まる.
■
証明
5点が一般の位置にあるときは命題82そのものである.
3点が同一直線上にあるときは,その3点で定まる直線と,
他の2点で定まる直線に分解した二次曲線 が一意に定まる.
4点が1直線上にあるときは,
その4点で定まる直線と,他の1点を通る直線に分解した
二次曲線なので,一意に定まらない.
□
が一意に定まる.
4点が1直線上にあるときは,
その4点で定まる直線と,他の1点を通る直線に分解した
二次曲線なので,一意に定まらない.
□
パスカルの定理を次の形で再掲する.
本書では基本的に射影空間の点は小文字で,
ユークリッド空間の点は大文字で表すようにしている.
ただ代数的な証明では変数との区別を明確にするために,
点を大文字で表す.
同次座標
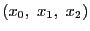 に対し,
に対し,
 で
で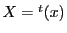 を表すものとする.
つまり
を表すものとする.
つまり は縦ベクトルにとる.他の文字についても同様とする.
は縦ベクトルにとる.他の文字についても同様とする.
また3次対称行列 に対し,
に対し,
とおく. が定める二次曲線を
が定める二次曲線を とし,
とし,
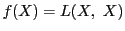 とおく.
とおく.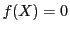 が
が の方程式,
の方程式,
 上の点
上の点 に対し
に対し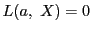 は点
は点 での接線の方程式,
での接線の方程式,
 上にない点
上にない点 に対し
に対し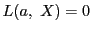 は点
は点 の極線の方程式である.
の極線の方程式である.
2次の同次式で定まる二次曲線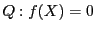 の上に異なる6点
の上に異なる6点
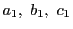 と
と
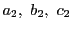 を取る.
を取る.
直線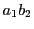 と直線
と直線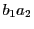 の交点を
の交点を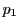 ,
直線
,
直線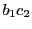 と直線
と直線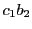 の交点を
の交点を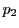 ,
直線
,
直線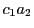 と直線
と直線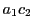 の交点を
の交点を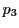 とする.
とする.
このとき3点
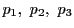 は一直線上にある.
■
は一直線上にある.
■
証明
点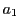 での接線と
での接線と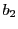 での接線の交点を
での接線の交点を
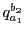 とかくと,
直線
とかくと,
直線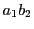 は
は
と表せる.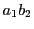 上の点はこの方程式を満たす.以下同様に記号を定める.
上の点はこの方程式を満たす.以下同様に記号を定める.
そこで,次の二次式を満たす曲線
を考える.
これは
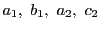 を通る.ここで,
を通る.ここで,
とおく.
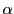 をこのようにとると
をこのようにとると 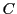 は
は 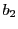 も通る.
も通る.
補題17から, と
と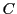 は同一の曲線となる.
は同一の曲線となる.
同様に次の二次式を満たす曲線
を考える.
これは
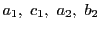 を通る.ここで,
を通る.ここで,
とおく.
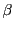 をこのようにとると
をこのようにとると 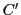 は
は 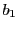 も通る.
従って同様の理由で
も通る.
従って同様の理由で 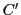 は
は  と一致する.
と一致する.
二つの二次曲線の同次式は定数倍を除いて一致する.
つまり
この両辺の二次式を考える.
左辺に 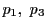 を代入すると0になるので,右辺も満たす.
そして
を代入すると0になるので,右辺も満たす.
そして 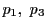 は
は
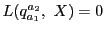 上にはない.よって,
上にはない.よって,
の上にある. 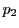 は明らかにこの式を満たす.
ここで,
は明らかにこの式を満たす.
ここで,
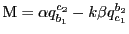 と置くとこの式は
と置くとこの式は
と表される.
つまり
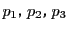 はすべて 直線
はすべて 直線
 の上にある.
□
の上にある.
□
2014-01-03
![]() に対し,
に対し,
![]() で
で![]() を表すものとする.
つまり
を表すものとする.
つまり![]() は縦ベクトルにとる.他の文字についても同様とする.
は縦ベクトルにとる.他の文字についても同様とする.
![]() に対し,
に対し,
の上に異なる6点
と
を取る.
と直線
の交点を
, 直線
と直線
の交点を
, 直線
と直線
の交点を
とする.
は一直線上にある. ■
![]() と
と![]() は同一の曲線となる.
は同一の曲線となる.
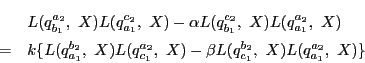
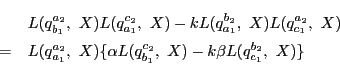
![]() を代入すると0になるので,右辺も満たす.
そして
を代入すると0になるので,右辺も満たす.
そして ![]() は
は
![]() 上にはない.よって,
上にはない.よって,