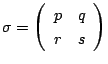 のとき,
のとき,
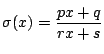 と書こう.
と書こう.
![]() であるような2次行列の全体を
であるような2次行列の全体を
![]() と書こう.
と書こう.
![]() が
が
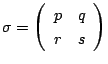 のとき,
のとき,
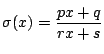 と書こう.
と書こう.
判別式の![]() に対する不変性の確認は,
に対する不変性の確認は,![]() で考えても
で考えても
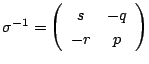 で考えても同じことだった.
ここはもういちど最初の変換に立ちかえって考えよう.
で考えても同じことだった.
ここはもういちど最初の変換に立ちかえって考えよう.
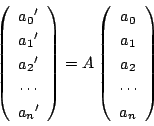
この対応で,
![]() が
が
![]() に対応しているとし,
に対応しているとし,
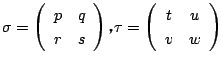 とする.
とする.
![]() を
を![]() で変換し,続いてそれを
で変換し,続いてそれを![]() で変換して得られる
係数はどのようになるか.
で変換して得られる
係数はどのようになるか.
耕介
まず![]() を
を
![]() で定めます.
で定めます.
これを![]() で変換すると
で変換すると
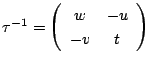 なので
なので
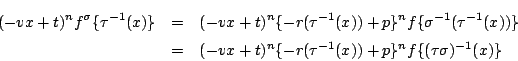
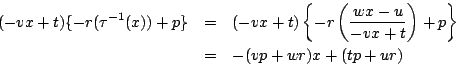
南海 不変性を確認するときはどちらでもよいのだが, 順序を保とうとすると注意しなければならない.
耕介
これに対して係数の変換は
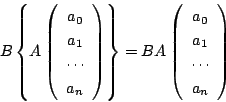
南海
このようにして定まる写像
![]() の判別式は係数
の判別式は係数
![]() の整式であった.
つまり
の整式であった.
つまり
耕介 なるほど.
南海
これは![]() の
の![]() への表現を通した判別式への作用なのだが,
要するに
への表現を通した判別式への作用なのだが,
要するに![]() の像である
の像である![]() の部分群
の部分群![]() が
が
![]() 個の文字
個の文字
![]() に作用し,
その変換で判別式を変換すると,判別式が不変になった.
そこで,次のように不変式を定義しよう.
ただしここでも積が保たれるように,作用させ方を工夫しておく.
に作用し,
その変換で判別式を変換すると,判別式が不変になった.
そこで,次のように不変式を定義しよう.
ただしここでも積が保たれるように,作用させ方を工夫しておく.
一般に![]() 変数の多項式
変数の多項式
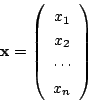
逆行列をもつ![]() 次行列の集合
次行列の集合![]() を考え,その部分群
を考え,その部分群![]() をとる.
をとる.
![]() の要素
の要素![]() に対してこれを右からかけた
に対してこれを右からかけた
![]() は各要素が
は各要素が
![]() の1次結合でできたベクトルだ.
の1次結合でできたベクトルだ.
![]() の各成分をもとの
の各成分をもとの
![]() に代入して得られる
多項式
に代入して得られる
多項式
![]() を
を
![]() と書こう.
と書こう.
まず![]() を作用させ
を作用させ
![]() を作り,
この多項式に
を作り,
この多項式に![]() を作用させる.
すると
を作用させる.
すると
作用のさせ方はいろんな方式があるのだが, 不変であるということに関しては,いずれでも変わらない. だから不変性を考えるかぎり混乱は起こらない.