南海
さらに判別式と終結式の関係を明示的に書くには
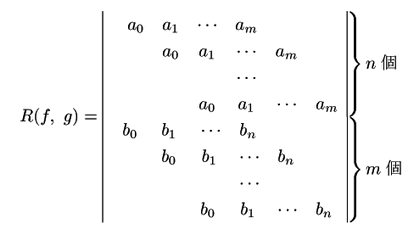
行列式による終結式と判別式の表示が必要だ.
一般の![]() 次行列式の理解が必要だが,これは
『線型代数の考え方』を見てほしい.
次行列式の理解が必要だが,これは
『線型代数の考え方』を見てほしい.
さて行列式を用いると終結式を係数を用いて具体的に書くことができる.
証明
![]() ,
,![]() が
が
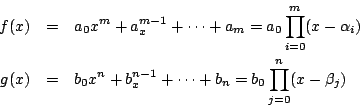
ある![]() とある
とある![]() に共通の不定元
に共通の不定元![]() を代入する.
すると
を代入する.
すると
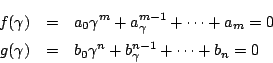
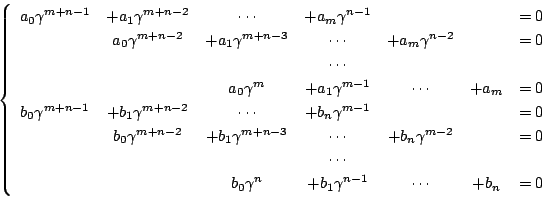
耕介
係数は根と![]() や
や![]() で書けているので
行列式,
で書けているので
行列式,

そのうちの
ある![]() とある
とある![]() に共通の不定元
に共通の不定元![]() を代入すると,
この行列式が0になるということですね.
を代入すると,
この行列式が0になるということですね.
南海
そういうことだ.そしてこれが任意の![]() と
と![]() についていえる.したがってこの行列式は,
すべての
についていえる.したがってこの行列式は,
すべての
![]() で割りきれる.
で割りきれる.
各
![]() と
と
![]() はそれぞれ
はそれぞれ
![]() と
と![]() で割りきれる(根と
で割りきれる(根と![]() や
や![]() との積になっている).
よって
との積になっている).
よって![]() は
は
![]() で割りきれる.
したがって
で割りきれる.
したがって![]() は
は![]() で割りきれる.
で割りきれる.
一方行列![]() を展開すると,その項は
を展開すると,その項は
それが0でないとき,その項の根から見た次数は
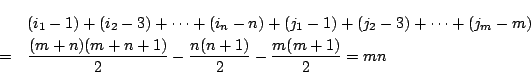
これは
![]() には
には
![]() という項がある.
一方,
という項がある.
一方,![]() の対応する項は
の対応する項は
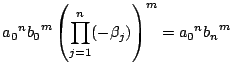 である.よって
である.よって![]() となり,定理の等式が示された.
□
となり,定理の等式が示された.
□
耕介
例(1.2)をこの方法で求めてみます.
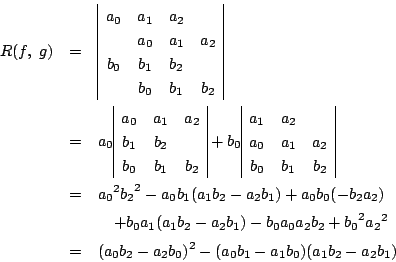
南海 判別式と終結式の間に定理3の関係があった.
これをもとに,判別式を終結式の行列表現から求めることができる. 例(1.1)を行列式でやってみてほしい.
耕介
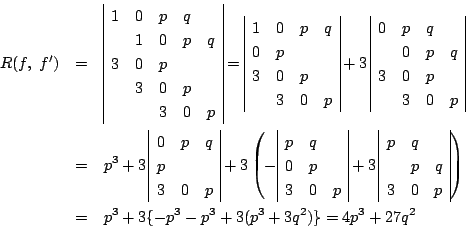
不変式の計算は大変です.
南海 ところがフリーソフトのRisa/Asir などを使うと, 終結式や因数分解がすぐに出来る.
前に掲示板で
という質問があった. 次のように出来る.から,
を求めようとしましたが, 解けませんでした
![\begin{displaymath}
\begin{array}{l}
[0]\mathrm{res}(b,b^3-3*a^2*b+11,3*a*...
...^2+8*a+1,1],[16*a^4-32*a^3+60*a^2-8*a+1,1]]
\end{array}
\end{displaymath}](images/img328.gif)
最初の[0]で![]() 終結式を用いて
終結式を用いて![]() を消去している.
次に
を消去している.
次に![]() を定義し,最後にそれを因数分解している.
を定義し,最後にそれを因数分解している.
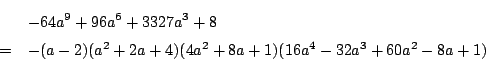
耕介 すごいですね.どこで手に入りますか.
南海 例えば,『Risa/Asir (神戸版) ダウンロードページ』などいくつかある.