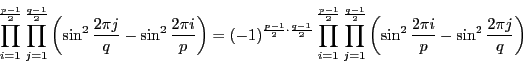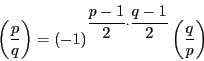次: 演習問題
上: いくつかの別証明
前: ガウス和を用いる証明
次: 演習問題
上: いくつかの別証明
前: ガウス和を用いる証明
平方剰余の相互法則のもう一つの証明を,
『数論講義』(J.P,Serre,岩波書店)に沿いつつそれを初等化して行う.
G.Eisenstein,F.が 1845 年に発表したもので,ある三角法の補題を用いる.
ガウスの予備定理34は前提にする.
その後の初等的な座標による証明の部分に対する別証明を与えるものである.
補題 5 (三角法の補題)
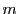
を奇素数とする.等式
が成り立つ.■
証明
ド・モアブルの定理と二項定理により,
が成立する.虚数部分を比較して
となる.
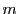 が奇素数なので
が奇素数なので 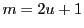 とおくと
とおくと
したがって,
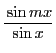 は
は 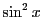 の多項式で,
その次数は
の多項式で,
その次数は
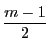 であり,さらに最高次数の係数は
であり,さらに最高次数の係数は
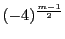 となることがわかる.
となることがわかる.
一方,
に対して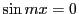 であり,
であり,
はすべて異なる.ゆえに
と分解される.つまり補題が示された.
□
定理33(再掲)
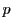 と
と 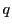 を相異なる2つの奇素数とする.
を相異なる2つの奇素数とする.
が成り立つ.■
証明
に対して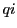 を考える.
それらを
を考える.
それらを 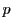 で割った余りが
で割った余りが 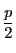 を超えるものの個数を
を超えるものの個数を  とする.
とする.
 は
は
のうち負になるものの個数である.さらにこれらはガウスの予備定理
34
の証明にあるように符号を除けば
と一致する.
ガウスの予備定理34
より
なので,三角法の補題5
を
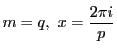 で用いることにより
で用いることにより
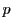 と
と 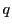 を入れ替えれば
を入れ替えれば
ところがこの積は合計
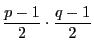 個にわたるものであるから
個にわたるものであるから
したがって
つまり
が示された.□


 次: 演習問題
上: いくつかの別証明
前: ガウス和を用いる証明
Aozora Gakuen
次: 演習問題
上: いくつかの別証明
前: ガウス和を用いる証明
Aozora Gakuen
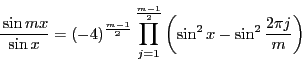
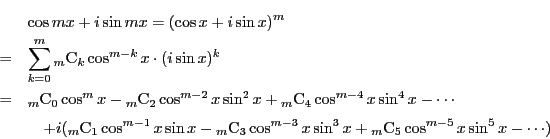
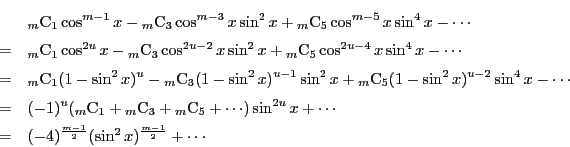
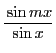 は
は 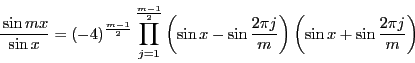
![]() と
と ![]() を相異なる2つの奇素数とする.
を相異なる2つの奇素数とする.
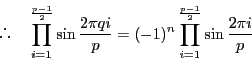
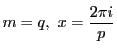 で用いることにより
で用いることにより
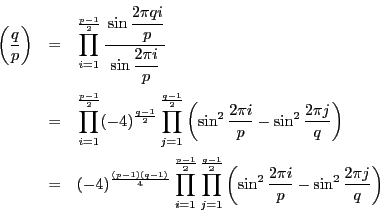
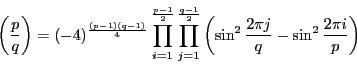
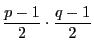 個にわたるものであるから
個にわたるものであるから