

 次: 三角法の補題による証明
上: いくつかの別証明
前: いくつかの別証明
次: 三角法の補題による証明
上: いくつかの別証明
前: いくつかの別証明
ここでいわゆるガウス和を用いて平方剰余の相互法則(定理33の(1))の証明を行う.
今日ガウス和を用いた証明は,「有限体の指標」の問題としてガロア理論を土台にして行われるが,
ここではガロア理論も有限体や巡回群の理論も仮定せずに,
もっとも最初になされたように初等整数論の範囲内で行う.
 を奇素数とし,
を奇素数とし, 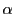 を1の原始
を1の原始  乗根とする.具体的には例えば
乗根とする.具体的には例えば
とする.
このときガウス和 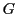 とは
とは
のことをいう.
この和の2乗 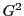 を二通りの方法で計算することによって,
相互法則が示される.定理33(1)の
証明では(2)第一補充則と(3)第二補充則を先に示し,その結果を(1)平方剰余の相互法則の
証明に用いた.同様にここでも,(2)第一補充則と(3)第二補充則は示されているものとする.
を二通りの方法で計算することによって,
相互法則が示される.定理33(1)の
証明では(2)第一補充則と(3)第二補充則を先に示し,その結果を(1)平方剰余の相互法則の
証明に用いた.同様にここでも,(2)第一補充則と(3)第二補充則は示されているものとする.
ガウス和を明示的に書くために,原始根を用いる.
 を
を  を法とする剰余系の原始根とする.定理28によって,原始根は存在する.
を法とする剰余系の原始根とする.定理28によって,原始根は存在する.
が既約剰余系の一組になる.定理30の証明冒頭と同様の理由で, 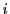 が偶数か奇数に
したがって
が偶数か奇数に
したがって
である.ゆえにガウス和 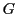 は原始根
は原始根  を用いれば
を用いれば
と明示的に書くことができる.
ここで
とおく.
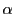 は
は
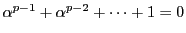 であるから
であるから
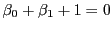 .
.
であるから 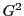 を計算するためには,
を計算するためには,
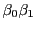 が確定すればよい.
が確定すればよい.
例 3.3.1
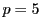
のとき.3は5を法とする原始根である.実際
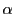
を1の原始5乗根とする.
例 3.3.2
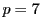
のとき.3は7を法とする原始根である.実際
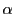
を1の原始7乗根とする.
この例を一般化して示すために1のべき根の性質で必要なものをまとめておく.
補題 3
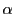
を1の原始

乗根,

を

を法とする原始根とする.
- (1)
- 有理数
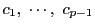 を用いて
を用いて
となるなら,
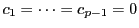 である.
である.
- (2)
- 有理数
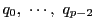 を用いて
を用いて
とおく.
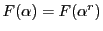 ならば
ならば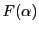 は有理数である.
■
は有理数である.
■
証明
- (1)
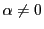 より
より
となるが, 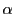 は1の原始
は1の原始  乗根なので
乗根なので 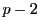 以下の次数の方程式の
解とはならない.ゆえに
以下の次数の方程式の
解とはならない.ゆえに
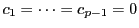 である.
である.
- (2)
-
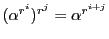 である.
である.
は既約剰余系で,
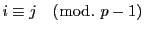 なら
なら
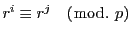 となる.したがって
となる.したがって
に 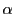 を代入したものと,
を代入したものと,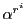 を代入したものは,1の
を代入したものは,1の  乗根で
1以外のものが順序が
乗根で
1以外のものが順序が 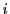 番ずれて現れる.
(1)から既約剰余系の有理数係数の一次結合による複素数の表示は一意である.
ゆえに
番ずれて現れる.
(1)から既約剰余系の有理数係数の一次結合による複素数の表示は一意である.
ゆえに
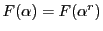 のとき,
のとき,
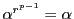 より
より
となり,
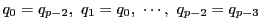 と,対応する係数
と,対応する係数 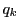 が順次等しくなる.
が順次等しくなる.
である.
となり,確かに有理数である.□
さて, 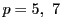 の計算は次の結果を推測させたが,それを示そう.
の計算は次の結果を推測させたが,それを示そう.
定理 35
記号はこの節の通りとする.このとき
となる.■
証明
フェルマの小定理から
である.ゆえに
したがって,整数  に対して
に対して
次に
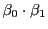 において
において 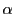 の代わりに
の代わりに 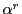 を代入すると
を代入すると
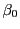 と
と 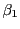 が入れ替わるので
が入れ替わるので
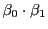 は変わらない.
したがって補題から
は変わらない.
したがって補題から
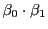 は有理数である.
は有理数である.
また有理数
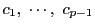 に対して
に対して
が有理数となるのは
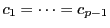 のときにかぎる.それ以外にあれば,
のときにかぎる.それ以外にあれば,
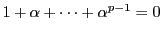 とあわせて
とあわせて 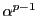 の項を消せば,
の項を消せば, 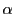 が
が
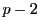 次以下の方程式を満たすことになるからである.
次以下の方程式を満たすことになるからである.
そこで
- (i)
-
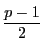 が奇数.つまり
が奇数.つまり
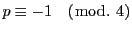 のとき.
のとき.
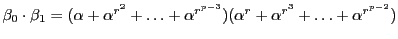 を展開した段階でできる
を展開した段階でできる
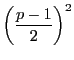 個の積のうち,1になるものが
個の積のうち,1になるものが
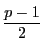 個あり,
残る
個あり,
残る
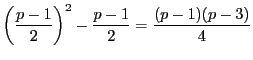 個の和は有理数なので,
それら
個の和は有理数なので,
それら 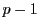 個ずつ
個ずつ
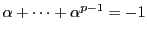 でまとめられ,それが
でまとめられ,それが
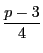 個ある.
個ある.
- (ii)
-
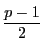 が偶数.つまり
が偶数.つまり
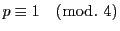 のとき.
のとき.
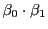 を展開した段階でできる
を展開した段階でできる
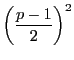 個の積のうちに1になるものはなく,すべて
個の積のうちに1になるものはなく,すべて
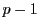 個ずつ
個ずつ
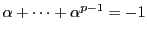 でまとめられる.
でまとめられる.
これで補題が示された.□
これから 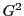 が計算でき,他の計算と比較して相互法則が示される.
証明の中で用いる補題を先に証明しておく.
が計算でき,他の計算と比較して相互法則が示される.
証明の中で用いる補題を先に証明しておく.
補題 4
素数

と整数係数の多項式
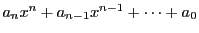
に対して
である.■
証明
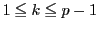 に対して
に対して
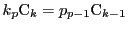 より
より
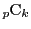 は
は  の倍数.
の倍数.
である.□
定理 36 (平方剰余の相互法則の別証明)

を

と異なる奇素数とする.複合を
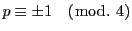
と同順にとって
である.■
証明
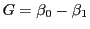 であるから,上の定理から
であるから,上の定理から
オイラーの規準(定理31)から
であるから
つまり
一方
つまり
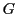 において
において
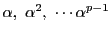 の係数はすべて
の係数はすべて 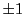 であるから,
であるから,
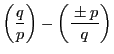 がすべて
がすべて  の倍数になる.
の倍数になる.
これがとりうる値は 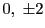 であるが
であるが  が奇素数なので
が奇素数なので
でなければならない.□
これはすなわち平方剰余の相互法則である.
ここではガウス和 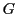 の平方のみを用いた.
の平方のみを用いた. 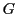 そのものは使わなかったので,
そのものは使わなかったので, 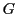 の符号を決定する必要がなかった.
の符号を決定する必要がなかった. 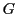 の符号を決定するのは簡単ではない.
の符号を決定するのは簡単ではない.


 次: 三角法の補題による証明
上: いくつかの別証明
前: いくつかの別証明
Aozora Gakuen
次: 三角法の補題による証明
上: いくつかの別証明
前: いくつかの別証明
Aozora Gakuen
![]() を奇素数とし,
を奇素数とし, ![]() を1の原始
を1の原始 ![]() 乗根とする.具体的には例えば
乗根とする.具体的には例えば
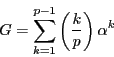
![]() を二通りの方法で計算することによって,
相互法則が示される.定理33(1)の
証明では(2)第一補充則と(3)第二補充則を先に示し,その結果を(1)平方剰余の相互法則の
証明に用いた.同様にここでも,(2)第一補充則と(3)第二補充則は示されているものとする.
を二通りの方法で計算することによって,
相互法則が示される.定理33(1)の
証明では(2)第一補充則と(3)第二補充則を先に示し,その結果を(1)平方剰余の相互法則の
証明に用いた.同様にここでも,(2)第一補充則と(3)第二補充則は示されているものとする.
![]() を
を ![]() を法とする剰余系の原始根とする.定理28によって,原始根は存在する.
を法とする剰余系の原始根とする.定理28によって,原始根は存在する.
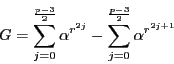
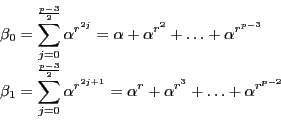
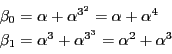
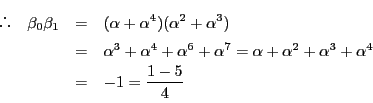
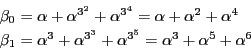
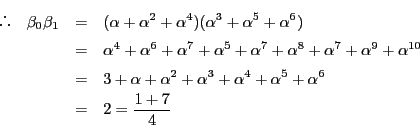
![]() の計算は次の結果を推測させたが,それを示そう.
の計算は次の結果を推測させたが,それを示そう.
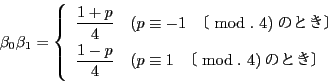
![]() において
において ![]() の代わりに
の代わりに ![]() を代入すると
を代入すると
![]() と
と ![]() が入れ替わるので
が入れ替わるので
![]() は変わらない.
したがって補題から
は変わらない.
したがって補題から
![]() は有理数である.
は有理数である.
![]() に対して
に対して
![]() を展開した段階でできる
を展開した段階でできる
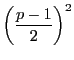 個の積のうち,1になるものが
個の積のうち,1になるものが
![]() 個あり,
残る
個あり,
残る
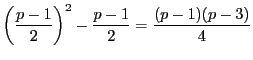 個の和は有理数なので,
それら
個の和は有理数なので,
それら ![]() 個ずつ
個ずつ
![]() でまとめられ,それが
でまとめられ,それが
![]() 個ある.
個ある.
![]() を展開した段階でできる
を展開した段階でできる
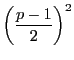 個の積のうちに1になるものはなく,すべて
個の積のうちに1になるものはなく,すべて
![]() 個ずつ
個ずつ
![]() でまとめられる.
でまとめられる.
![]() が計算でき,他の計算と比較して相互法則が示される.
証明の中で用いる補題を先に証明しておく.
が計算でき,他の計算と比較して相互法則が示される.
証明の中で用いる補題を先に証明しておく.
![]() に対して
に対して
![]() より
より
![]() は
は ![]() の倍数.
の倍数.
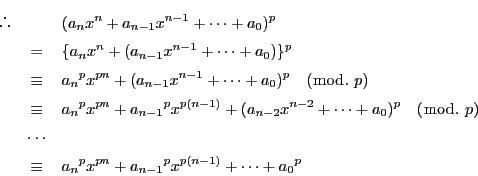
![]() であるから,上の定理から
であるから,上の定理から
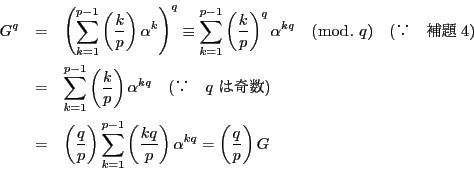
![]() において
において
![]() の係数はすべて
の係数はすべて ![]() であるから,
であるから,
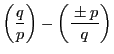 がすべて
がすべて ![]() の倍数になる.
の倍数になる.
![]() であるが
であるが ![]() が奇素数なので
が奇素数なので
![]() の平方のみを用いた.
の平方のみを用いた. ![]() そのものは使わなかったので,
そのものは使わなかったので, ![]() の符号を決定する必要がなかった.
の符号を決定する必要がなかった. ![]() の符号を決定するのは簡単ではない.
の符号を決定するのは簡単ではない.