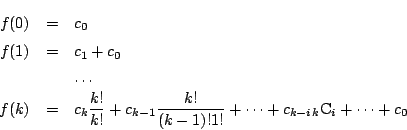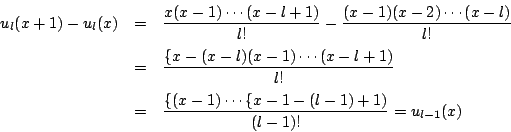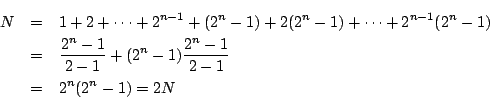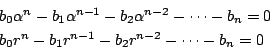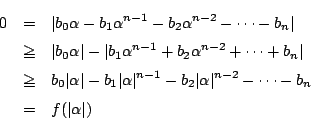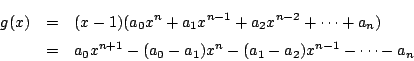-
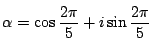 とおく.このとき,
とおく.このとき,
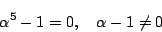
なので
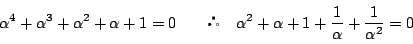
つまり,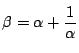 とおくと,
とおくと,
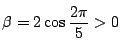 であり, かつ
であり, かつ
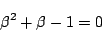
よって,
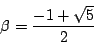
となり,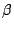 は無理数である.
は無理数である.
いま,題意の余りは明らかに四次以下の整式であるから, これを
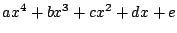 とおくと,
とおくと,
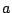 ,
, 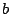 ,
, 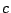 ,
, 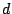 ,
, 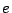 は明らかに有理数で,
は明らかに有理数で,
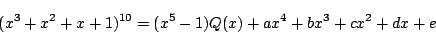
と表される.この両辺に
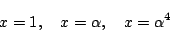
を代入する.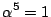 に注意して整理すると,
に注意して整理すると,
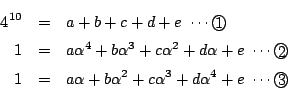
そこで,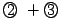 をとる.
をとる.
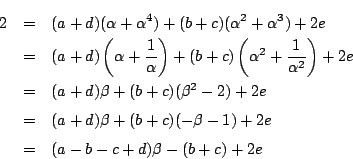
で,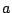 ,
, 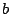 ,
, 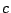 ,
, 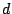 は有理数だから,
は有理数だから,
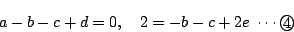
次に,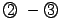 をとる.
をとる.
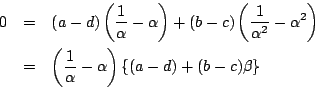
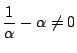 だから,
だから,
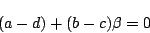
よって,
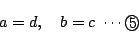
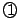 ,
, 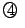 ,
, 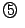 から
から
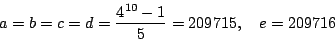
を得る.つまり,求める余りは
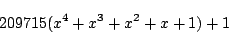
- 求める余りを
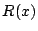 ,そのときの商を
,そのときの商を 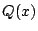 とする.つまり
とする.つまり
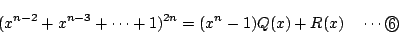
ここで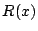 の次数は
の次数は 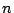 より小さい.
より小さい.
また
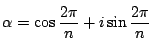 とおく.
とおく.
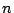 個の複素数
個の複素数
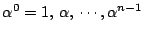 はすべて異なり,
はすべて異なり,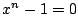 を満たす.よってこれらが
を満たす.よってこれらが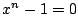 の解の全体である.
したがって次の因数分解が成り立つ.
の解の全体である.
したがって次の因数分解が成り立つ.
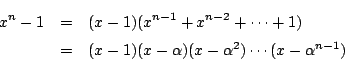
つまり
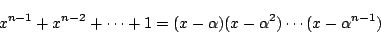
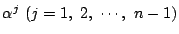 を
を
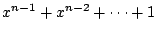 に代入すると0なので,
に代入すると0なので,
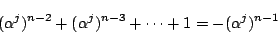
ゆえに6に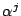 を代入すると左辺は常に1である.つまり
を代入すると左辺は常に1である.つまり
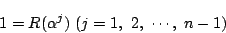
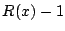 は
は 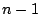 次以下であるから,因数定理によって
次以下であるから,因数定理によって
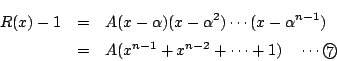
とかける.ここに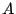 は定数である.
は定数である.
一方6に
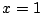 を代入することにより
を代入することにより
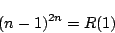
また7に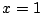 を代入することにより
を代入することにより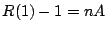
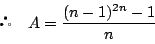
したがって求める余り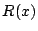 は
は
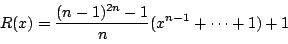
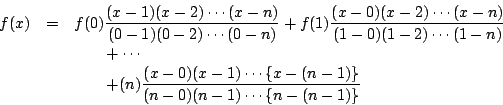
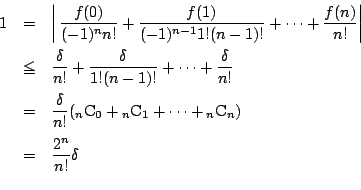
![\begin{eqnarray*}
f(x)&=&\dfrac{n!}{2^n}\left[ \dfrac{(x-1)(x-2) \cdots (x-n)}{...
...!}+ \cdots
+ \dfrac{x(x-1)(x-2) \cdots \{x-(n-1)\}}{n!}\right]
\end{eqnarray*}](images/img104.gif)
![\begin{eqnarray*}
f(x+1)-f(x)&=&a_n(x+1)^n-a_nx^n+[ n-1以下の項のみ ] \\
&=&a_n(nx^{n-1}+\cdots)+[ n-1以下の項のみ ]
\end{eqnarray*}](images/img106.gif)