1番の玉が赤である事象を![]() ,
3番の玉が白である事象を
,
3番の玉が白である事象を![]() とする.
とする.
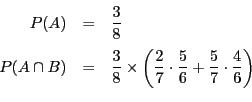
事象![]() と事象
と事象![]() が独立となるということは
が独立となるということは
![\begin{displaymath}
P(A\cap B)=\dfrac{\left[\dfrac{m}{2}\right]}{6}
\end{displaymath}](images/img342.gif)
従って求める確率は
領域
従って求める確率は
![]() の体積を求める.
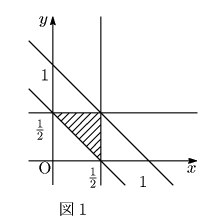
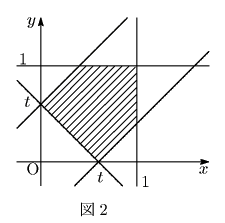
の体積を求める. ![]() での切断面は図2のようになりその面積は
での切断面は図2のようになりその面積は
従って求める確率は
![]() の面積(境界を含む)は,
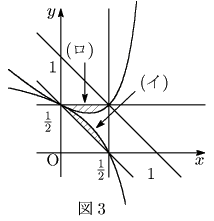
の面積(境界を含む)は, ![]() の面積から,図3の領域(イ)一つ,と領域(ロ)を二つ分を減じたものである.
の面積から,図3の領域(イ)一つ,と領域(ロ)を二つ分を減じたものである.
(イ)の面積は
![\begin{displaymath}
\int_0^{ \frac{1}{2}}\left(\dfrac{1}{2}+x- \dfrac{1}{2-2x}\...
...x) \right]_0^{ \frac{1}{2}}
=\dfrac{3}{8}-\dfrac{1}{2}\log 2
\end{displaymath}](images/img373.gif)
ゆえに ![]() の面積は
の面積は
従って3本の線分が鋭角三角形を作る確率は
![]() の体積(境界を含む)をもとめる.
の体積(境界を含む)をもとめる. ![]() での切断面において,
での切断面において, ![]() の切断面から,
図4の領域(ハ)一つ,と領域(ニ)を二つ分を減じたものである.
の切断面から,
図4の領域(ハ)一つ,と領域(ニ)を二つ分を減じたものである.
(ハ)の面積は
ゆえに ![]() の面積は
の面積は ![]() の体積が
の体積が ![]() であったので,
であったので,
従って3本の線分が鋭角三角形を作る確率は