1.
-
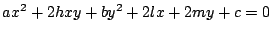 �̗��ӂ�
�̗��ӂ� 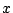 �Ŕ��������
�Ŕ��������
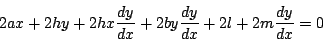
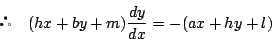
����������, �_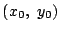 �ɂ�����ڐ��̕�������
�ɂ�����ڐ��̕�������
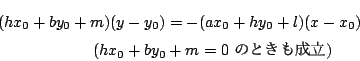
�����ŁC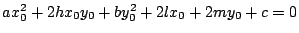 ���
���
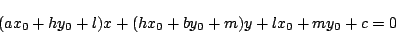
�����
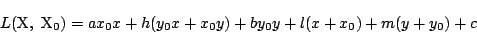
������, ���̂Ƃ�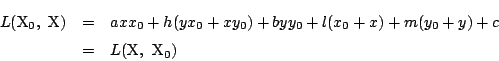
-
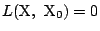 ��
��
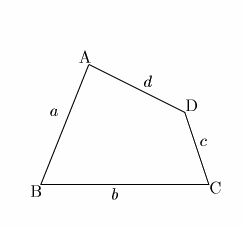
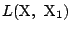 �̌�_��P�Ƃ����(�}1)�C
�̌�_��P�Ƃ����(�}1)�C
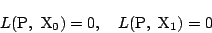
���C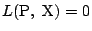 �͒���
�͒���
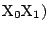 �̕�������\���D
�̕�������\���D
���Ȃ킿�C
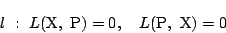
1.
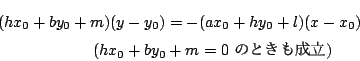
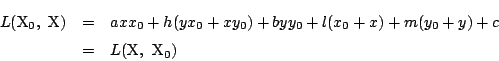
���Ȃ킿�C
Q�� ![]() ��ɂ���̂�
��ɂ���̂�
2.
���Ȃ킿, �^����ꂽ�������͂���2�_��ʂ�ꎟ���ł��邩��C ���̒����̕������ɑ��Ȃ�Ȃ�.
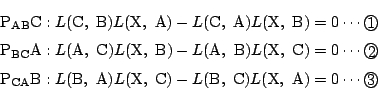
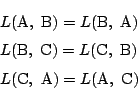
�܂�, ��_��
![]() ��ɂ�����̂�, �����3�̒�����1�_�Ō����.
��ɂ�����̂�, �����3�̒�����1�_�Ō����.
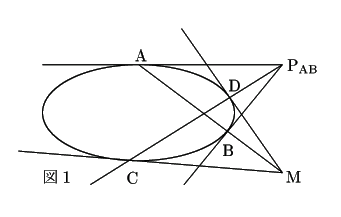 AB ��
AB ��
���l��, BC �� ![]() �̌�_ N �ɑ���,
�̌�_ N �ɑ���,
![]() �͏��
�͏�� ![]() �ƈ�v��, CA ��
�ƈ�v��, CA �� ![]() �̌�_ K �ɑ�,
�̌�_ K �ɑ�,
![]() �͏��
�͏�� ![]() �ƈ�v����. ������,
�����3�̒����͂��ׂ� P ��ʂ�̂�
�ƈ�v����. ������,
�����3�̒����͂��ׂ� P ��ʂ�̂�
1�D�x�N�g���̌v�Z�Œ����ɂ킩��W���D
 �}�̂悤��
�}�̂悤��
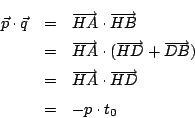
![]() �̖ʐ�
�̖ʐ�![]() �͎��̂悤�ɕ\�����D
�͎��̂悤�ɕ\�����D
2�D���S�ƂȂ�Ƃ���}��ϐ��Ɋւ���ɒl�Ƃ��ĂƂ炦��D
 ����
����![]() �����肷�邽�߂ɁC���̐ݒ������D
�����肷�邽�߂ɁC���̐ݒ������D
![]() �̒����͗^����ꂽ���̂ɌŒ肵�C
�̒����͗^����ꂽ���̂ɌŒ肵�C
![]()
![]() ����
����![]() �ւ̐����̑���
�ւ̐����̑���![]() �Ƃ��C
�Ƃ��C![]() �Ƃ����D
�܂�
�Ƃ����D
�܂�![]() ��
��
![]() �������ɂȂ�悤�ɂƂ�D
�������ɂȂ�悤�ɂƂ�D
![]() �̖ʐς�}��ϐ�
�̖ʐς�}��ϐ�![]() �̊�
�̊�![]() �ƍl����D
���̂Ƃ����̂��Ƃ����藧�D
�ƍl����D
���̂Ƃ����̂��Ƃ����藧�D
![]() ���ő�̂Ƃ��C
���ő�̂Ƃ��C![]() ��
��
![]() �̐��S�ł���D
�̐��S�ł���D
�������S�łȂ����![]() ��
��![]() �Ɛ����ł͂Ȃ��D
�Ɛ����ł͂Ȃ��D
![]() ��
��![]() �ɐ�����
�ɐ�����
![]() �ɂƂ�D
�ɂƂ�D
 �Ƃ��낪���̂Ƃ��C�͂��߂̐ݒ�Ɠ���������
�Ƃ��낪���̂Ƃ��C�͂��߂̐ݒ�Ɠ���������
![]() ���ʐς̑傫���O�p�`��
�����Ă���̂ŁC
���ʐς̑傫���O�p�`��
�����Ă���̂ŁC
![]() ���ʐύő�̉���Ɩ�������D
����āC�ʐύő�̂Ƃ��C
���ʐύő�̉���Ɩ�������D
����āC�ʐύő�̂Ƃ��C![]() �͐��S�łȂ���Ȃ炸�C
�͐��S�łȂ���Ȃ炸�C
![]() �ł��邱�Ƃ��킩��D
�ł��邱�Ƃ��킩��D
����
��L�̍l�@���C![]() �ł��邩��C������Đ�������ƁC
�ł��邩��C������Đ�������ƁC
����2�悵�Ă܂Ƃ߂�ƁC
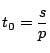 ��������ƁC
��������ƁC
����3���������́C3���̘a�����Őς����ł��邩��C���̎��������������܂�D
3�D�r���̂܂Ƃ߁D
�ŏ��̖��̉���3��������
������![]() �����߂邽�߂� 3���������������˂Ȃ�Ȃ��D
���̉�@�����C����́w���w�Θb�x�u����3�����̈���������3���������v���Q�Ƃ��Ă��炢�����D
��̓I�ɏ������Ƃ͂����ł͏ȗ�����D
�����߂邽�߂� 3���������������˂Ȃ�Ȃ��D
���̉�@�����C����́w���w�Θb�x�u����3�����̈���������3���������v���Q�Ƃ��Ă��炢�����D
��̓I�ɏ������Ƃ͂����ł͏ȗ�����D
�ʐύő�ł���̂�![]() �����S�łȂ��Ƃ���D�ΖʂƐ����łȂ�������
�����S�łȂ��Ƃ���D�ΖʂƐ����łȂ�������![]() �Ƃ���D
�Ƃ���D
![]() ��
��
![]() �i�������
�i�������
![]() �j
�ƂȂ�悤�ɂƂ�D����Ɓ@
�j
�ƂȂ�悤�ɂƂ�D����Ɓ@
![]() ��
��![]() O���畽��
O���畽��![]() �ւ̐����̑��Ƃ��A
�ւ̐����̑��Ƃ��A
![]() �����
�����![]() ��
��
![]() ���ʐύő�ɂȂ�悤
�Ɂi���Ȃ킿
���ʐύő�ɂȂ�悤
�Ɂi���Ȃ킿![]() ��
��
![]() �̐��S�ɂȂ�悤�Ɂj�Ƃ�D
������
�̐��S�ɂȂ�悤�Ɂj�Ƃ�D
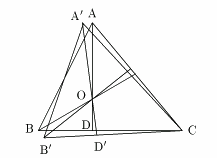
������![]() �̉������
�̉������![]() A'���Ƃ�D���̂Ƃ�
A'���Ƃ�D���̂Ƃ�
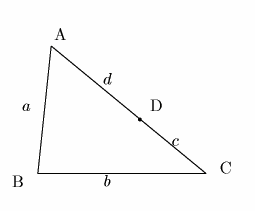
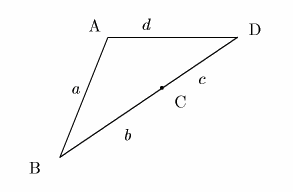
![]() �Ƃ���.
�Ƃ���.
�ʐς�
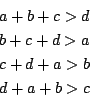
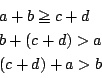
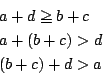
����������,
�}2����}3�֘A���I�ɕω������Ă����ƁC�A�����̒��Ԓl�̒藝����
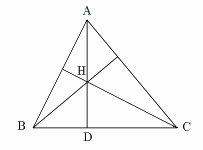
���ɁC $ \alpha+\beta=\pi $ �Ƃ���D $ \bigtriangleup \mathrm{ABC} $ �̊O�ډ~���Ƃ�C���̉~����ɓ_ $ \mathrm{E} $ �� $ \mathrm{BC} $ �Ɋւ��ċt�̑��ɂƂ�D 2�_ $ \mathrm{B}�C\mathrm{C} $ �Ɋւ���_ $ \mathrm{A} $ �Ɠ_ $ \mathrm{E} $ �̒��S�p�̘a�� $ 2\pi $ �Ȃ̂ŁC $ \angle \mathrm{E}=\pi-\alpha=\beta $ �ł���D ����āC $ \angle \mathrm{BEC}=\angle \mathrm{BDC} $ �ƂȂ�C �~���p�̒藝�̋t���C�_ $ \mathrm{D} $ �͂��̉~����ɂ���D
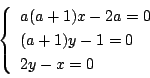
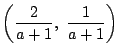 �͂���3�������ׂĖ������D�܂�
�͂���3�������ׂĖ������D�܂�
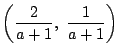 �͂���2�_��
�͂���2�_��
![]() ��̓_
��̓_ ![]() ��
�� ![]() ���ʏ�̓_
���ʏ�̓_ ![]() ��
��![]() �̓����_��
�̓����_��
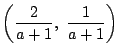 �ł���Ƃ���D����������
�ł���Ƃ���D����������
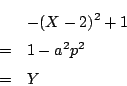
![]() ��
�� ![]() �͑����̒��S��
�͑����̒��S��
 �Ƃ��C
������
�Ƃ��C
������ ![]() �̑����ł���D
�̑����ł���D
�����������W���ʂɂ���,
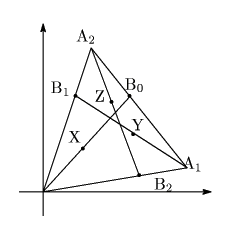
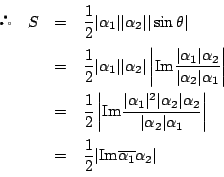
���� ![]() ��p����
��p����
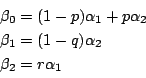
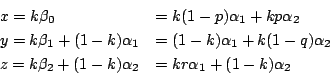
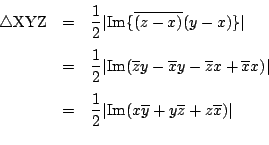

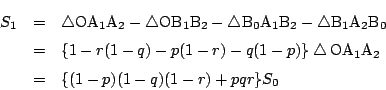
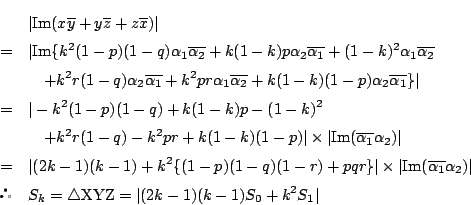
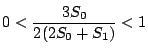 �ł���D
�ł���D
���s��2�ڐ��̕�������
![]() �̂Ƃ�
�̂Ƃ�![]() ���
���
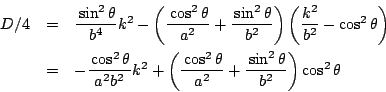
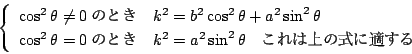
��ӂ����~�̒��S�͒���
![]() ��ɂȂ���Ȃ�Ȃ��D
��ɂȂ���Ȃ�Ȃ��D
���_���炱���̐ڐ��ւ̋����� ![]() �D
�D

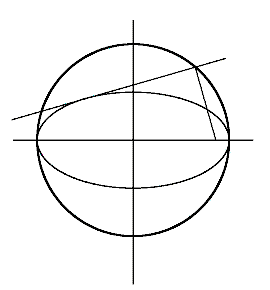
�Q�l
�ȉ~�����܂錴�_�𒆐S�Ƃ���~�ɂ͏�ŋ��߂����̂̑��Ɏ��̂悤�Ȃ��̂�����D
1.�œ_����ڐ��ւ̐����̑��̋O�ՁD![]()
2.����2�ڐ��̌�_�̋O�ՁD���~�Ƃ����D
![]()
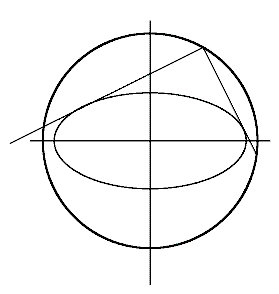
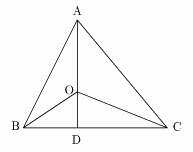
�����`�� ABCD �Ƃ���D���̏��ɍ�}����D
 A��C�CB��D �����ԁD��_��O�Ƃ���D
A��C�CB��D �����ԁD��_��O�Ƃ���D
C��D�����ѕӂ��̂��DCD ��Ő����`�̊O���̔C�ӂ̓_P<sub>0</sub>���Ƃ�D
�_![]() ��O�����сCAD�Ƃ̌�_��_��
��O�����сCAD�Ƃ̌�_��_��![]() �Ƃ���D
�_
�Ƃ���D
�_![]() ��C�����сCBD�Ƃ̌�_��_��
��C�����сCBD�Ƃ̌�_��_��![]() �Ƃ���D
�_
�Ƃ���D
�_![]() ��
��![]() �����сCAC�Ƃ̌�_��_��
�����сCAC�Ƃ̌�_��_��![]() �Ƃ���D
�_D��
�Ƃ���D
�_D��![]() �����сCBC�Ƃ̌�_��_��M�Ƃ���D
�����сCBC�Ƃ̌�_��_��M�Ƃ���D
���̂Ƃ� M �͕� BC�̒��_�ł���D
�Ȃ����D
O �����_�ɂ��CA![]() �CB
�CB![]() �CC
�CC![]() �CD
�CD![]() �ɂƂ�D
�ɂƂ�D
�_![]() ��O �����Ԓ�����
��O �����Ԓ����� ![]() �Ƃ����D
�������W�����߂�D
�Ƃ����D
�������W�����߂�D
(�����̎������߂�v�Z�͏ȗ�)
![]()
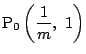
����
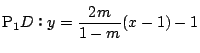 ���
���
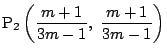
����
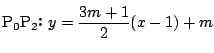 ���
���
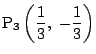
����
![]() ���M
���M![]()
���� ���̖��͐����`�łȂ��Ă��C�����������ɂȂ�C ���_�����_�ɂȂ�悤�ȕϊ��ŕό`���ꂽ�}�`�Ő��藧�D�Ⴆ�Ε��s�l�ӌ`�D
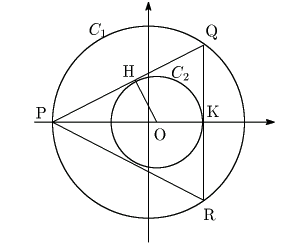
�~ ![]() �̒��S��
�̒��S�� ![]() �C
�C ![]() ����PQ�ւ̐����̑���H�CQR�Ɖ~
����PQ�ւ̐����̑���H�CQR�Ɖ~ ![]() �̐ړ_��K�Ƃ���D
�̐ړ_��K�Ƃ���D
![]() �C
�C
![]() �ł���D
�ł���D
������
![]() �̍��W��
�̍��W��
![]() �ł���D
�ł���D
�܂��C
![]() �ł��邩��
�ł��邩��
![]() �ƂȂ�D
�ƂȂ�D
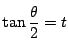 �ɂ����
�ɂ����
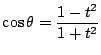 �C
�C
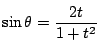 �ƕ\�����D
�ƕ\�����D
�䂦�ɉ~ ![]() ��̓_��
��̓_�� ![]() ��������
��������
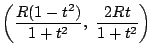 �ƕ\�����D
�ƕ\�����D
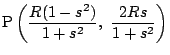 ��
��
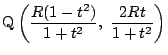 �̂Ƃ�
�̂Ƃ�
![]() �̌X����
�̌X����
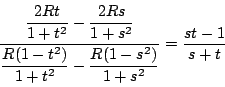
�䂦�ɒ��� ![]() �̕�������
�̕�������
���������Ē��� ![]() ���~
���~ ![]() �ɐڂ��邽�߂̏�����
�ɐڂ��邽�߂̏�����
�䂦�ɋ��߂� ![]() �̑�������
�̑�������
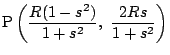 ����
�~
����
�~
1�� ![]() �Ő�������ƁC
�Ő�������ƁC
![]() �̂Ƃ�
�̂Ƃ�
![\begin{eqnarray*}
&&r^2\{(t_1t_2-1)^2+(t_1+t_2)^2\}
=\dfrac{r^2\{(R+a)^2s^2+(R...
...quad \quad \times[\{(R-a)(R+a)^2-2Rr^2\}s^2+(R-a)^2(R+a)-2Rr^2]
\end{eqnarray*}](images/img556.gif)
�䂦��
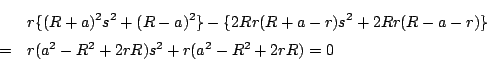
�m����3���������C
�C�ӂ̓_ ![]() �ɑ���
�ɑ���![]() �ƂȂ邱�Ƃ��������ꂽ�D
�ƂȂ邱�Ƃ��������ꂽ�D
![]() ��
��
![]() ��3�ӂ����ꂼ��
��3�ӂ����ꂼ��
![]() ��
��![]() �Ƃ���D�O�p�`�̐�����������
�Ƃ���D�O�p�`�̐�����������
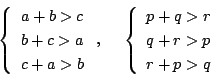
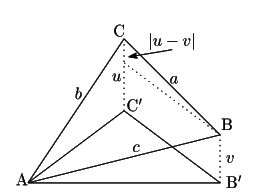
���s�ړ����ē_![]() �͕���
�͕���![]() ��ɂ���Ƃ��Ă悢�D������
����
��ɂ���Ƃ��Ă悢�D������
����
![]() �̒��������ꂼ��
�̒��������ꂼ��![]() �Ƃ���D
�Ƃ���D
���̂Ƃ�
![]() �̊e�ӂ�
�̊e�ӂ�
����������
![]() ��
��
![]() �������ɂȂ邱�Ƃ�
�������ɂȂ邱�Ƃ�
�܂�
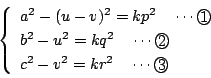
���āC![]() ��
��![]() �̒l��^����Ε���
�̒l��^����Ε���![]() ����܂�D
����������
����܂�D
����������
![]() ��
��
![]() �Ƒ����ɂȂ�悤�ȕ���
�Ƒ����ɂȂ�悤�ȕ���![]() �����݂��邱�Ƃ́C
�����݂��邱�Ƃ́C
![]() ��������
��������![]() �Ɛ���
�Ɛ���![]() �����݂��邱�Ɠ��l�ł���D
�����݂��邱�Ɠ��l�ł���D
![]() ���
���
���
![]() ���
���
![]() ����
����![]() �ɂ����
�ɂ����![]() �����������
�����������![]() ��2���������D
��2���������D
���̍��ӂ�![]() ��2�����Ƃ���
��2�����Ƃ���![]() �Ƃ����D
�Ƃ����D
![]() ��
��![]() ����
����![]() �����݂���C
�����݂���C![]() ���琳����������
���琳����������![]() ��
��![]() ����܂�D
����܂�D
![]() �ƂȂ�悤��
�ƂȂ�悤��![]() ��
��![]() �̐������߂�C��ӂ���
�̐������߂�C��ӂ���![]() ��
��![]() ��������D
��������D
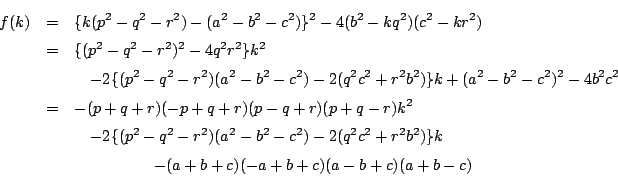
�O�p�`�̐�����������
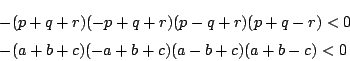
�܂�![]() �͏�ɓʂł���
�͏�ɓʂł���![]() �ł���D���
�ł���D���![]() �̒�`������
�̒�`������
�܂蕽��![]() �ŁC
�ŁC![]() �ւ̐��ˉe
�ւ̐��ˉe
![]() ��
��
![]() �Ƒ����ɂȂ���̂����݂��邱�Ƃ������ꂽ�D
�Ƒ����ɂȂ���̂����݂��邱�Ƃ������ꂽ�D